题目内容
6.已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为$\frac{\sqrt{2}}{2}$,又椭圆上任一点到两焦点的距离和为2$\sqrt{2}$.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.(1)求椭圆的方程;
(2)在线段OF上是否存在点M(m,0),使得|MP|=|MQ|?若存在,求出m的取值范围;若不存在,请说明理由.
分析 (1)根据椭圆的离心率,以及椭圆上任一点到两焦点的距离和为2$\sqrt{2}$,求出a,b,c即可求椭圆的方程;
(2)设出直线方程,联立直线方程和椭圆方程,转化为一元二次方程,利用根与系数之间的关系进行求解.
解答 解:(1)因为离心率为$\frac{\sqrt{2}}{2}$,
又2a=2$\sqrt{2}$.
∴a=$\sqrt{2}$,c=1.
∴b=1,
故椭圆的方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(2)①若l与x轴重合时,显然M与原点重合,即m=0符合条件,
②若直线l的斜率k≠0,
则可设l:y=k(x-1),
设P(x1,y1),Q(x2,y2),则:
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+2{y}^{2}-2=0}\end{array}\right.$得x2+2k2(x2-2x+1)-2=0,
化简得:(1+2k2)x2-4k2x+2k2-2=0;
即x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,即PQ的中点横坐标为:$\frac{2{k}^{2}}{1+2{k}^{2}}$,代入l:y=k(x-1)可得:
PQ的中点为N($\frac{2{k}^{2}}{1+2{k}^{2}},\frac{-k}{1+2{k}^{2}}$),
由于|MP|=|MQ|,得到m=$\frac{{k}^{2}}{2{k}^{2}+1}$
所以:m=$\frac{{k}^{2}}{2{k}^{2}+1}$=$\frac{1}{\frac{1}{{k}^{2}}+2}$$∈(0,\frac{1}{2})$,
综合(1)(2)得到:m$∈(0,\frac{1}{2})$.
点评 本题主要考查椭圆方程的求解以及直线和椭圆的位置关系的应用,利用设而不求的数学思想是解决本题的关键.

| A. | [-2$\sqrt{5}$,2$\sqrt{5}$] | B. | [0,2] | C. | [-2$\sqrt{5}$,2] | D. | [$\frac{2\sqrt{5}}{5}$,1] |
| A. | 相交 | B. | 平行 | C. | 异面 | D. | 不确定 |
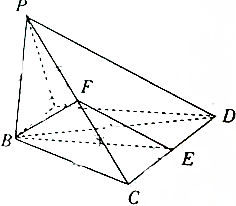 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.