题目内容
16.已知一元二次不等式ax2-2ax+2a-3<0(a≠0),求解下列问题:(1)当a=2时,解此不等式;
(2)若原不等式的解集为R,求实数a的取值范围.
分析 (1)将a代入不等式解之;
(2)利用判别式与系数的关系得到解集为R的等价条件.
解答 解:(1)a=2时,不等式为2x2-4x+1<0,化简为2(x-1)2<1,所以(x-1)2<$\frac{1}{2}$,所以1-$\frac{\sqrt{2}}{2}$<x<1+$\frac{\sqrt{2}}{2}$;
所以a=2时,不等式的解集为(1-$\frac{\sqrt{2}}{2}$,1$+\frac{\sqrt{2}}{2}$);
(2)原不等式的解集为R,
a≠0,原不等式的解集为R,等价于$\left\{\begin{array}{l}{a<0}\\{△=4{a}^{2}-4a(2a-3)<0}\end{array}\right.$,解得a>3或者a<0;
所以原不等式的解集为R,实数a的取值范围为a>3或者a<0.
点评 本题考查了一元二次不等式的解法以及一元二次不等式恒成立问题的处理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.a是平面α外的一条直线,过a作平面β,使β∥α,这样的β( )
| A. | 只有一个 | B. | 至少有一个 | C. | 不存在 | D. | 至多有一个 |
5.设命题p:不等式($\frac{1}{2014}$)x+4>m≥4x-x2对一切实数x恒成立,命题q:f(x)=-(9-2m)x是R上的增函数,若p且q为假命题,则实数m的取值范围是( )
| A. | {m|m≠4} | B. | {m|m∈R} | C. | {m|m≤0} | D. | {m|m≤0或m≥4} |
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1D上一定点且DP=2PA1,Q是AB1上一动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1D上一定点且DP=2PA1,Q是AB1上一动点.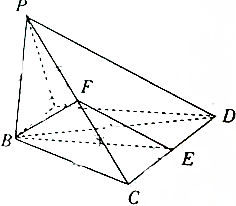 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.