题目内容
19.若锐角A,B满足:cosA=$\frac{4cos(A+B)}{5}$=$\frac{3}{5}$,求sinB.分析 先利用同角三角函数基本关系分别求得sinA和sin(A+B)的值,进而利用sinB=sin(A+B-A)通过两角和公式展开后求得答案.
解答 解:∵A,B均为锐角,
∴0<A+B<π,$cos(A+B)=\frac{3}{4}$,
∴sinA=$\sqrt{1-{cos}^{2}A}$=$\frac{4}{5}$,sin(A+B)=$\sqrt{1-{cos}^{2}(A+B)}$=$\frac{\sqrt{7}}{4}$,
∴sinB=sin(A+B-A)=sin(A+B)cosA-cos(A+B)sinA=$\frac{\sqrt{7}}{4}×\frac{3}{5}-\frac{3}{4}×\frac{4}{5}$=$\frac{3\sqrt{7}-12}{20}$.
点评 本题主要考查了两角和与差的正弦函数的应用.解题的关键是借助sinB=sin(A+B-A),利用两角和公式来解决问题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
9.已知实数x、y满足约束条件$\left\{\begin{array}{l}{xy≥0}\\{{x}^{2}+{y}^{2}≤4}\\{x+y-1≤0}\end{array}\right.$,则z=2x+y的取值范围是( )
| A. | [-2$\sqrt{5}$,2$\sqrt{5}$] | B. | [0,2] | C. | [-2$\sqrt{5}$,2] | D. | [$\frac{2\sqrt{5}}{5}$,1] |
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1D上一定点且DP=2PA1,Q是AB1上一动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1D上一定点且DP=2PA1,Q是AB1上一动点.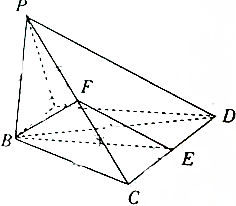 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.