题目内容
9．
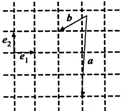已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示，以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底，则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$．
分析 用平面向量基本定理结合三角形法则即可得出正确的答案．
解答 解：根据图形得，
连接AB，则
$\overrightarrow{BA}$=$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{a}$-$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$．
故答案为：$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$．
点评 本题考查了平面向量的应用问题，也考查了作图能力的问题，是基础题目．
练习册系列答案
相关题目
20．若复数1-$\sqrt{3}i$（i为虚数单位），是z的共轭复数，则在复平面内，复数z对应的点的坐标为（ ）
| A． | （0，1） | B． | （1，-$\sqrt{3}$） | C． | （-1，-$\sqrt{3}$） | D． | （-1，0） |