题目内容
7.已知向量|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$.若向量$\overrightarrow m$满足|$\overrightarrow{m}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则$|{\overrightarrow m}$|的最大值是( )| A. | 2$\sqrt{3}$-1 | B. | 2$\sqrt{3}$+1 | C. | 4 | D. | $\sqrt{6}+\sqrt{2}$+1 |
分析 由题意结合数量积的几何意义画出图形,数形结合求得$|{\overrightarrow m}$|的最大值.
解答 解:如图,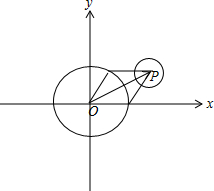
不妨设$\overrightarrow{a}=(2,0),\overrightarrow{b}=(1,\sqrt{3})$,则$\overrightarrow{a}+\overrightarrow{b}$=$(3,\sqrt{3})$,
∴满足|$\overrightarrow{m}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=1的$|{\overrightarrow m}$|的最大值是P(3,$\sqrt{3}$)到原点O的距离加1,
则$|{\overrightarrow m}$|的最大值是$\sqrt{{3}^{2}+(\sqrt{3})^{2}}+1=2\sqrt{3}+1$.
故选:B.
点评 本题考查平面向量的数量积运算,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
15.实数X,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+3y-3≥0\\ 3x+y-9≤0\end{array}\right.$,若z=ax+y的最大值为2a+3,则a的取值范围是( )
| A. | [-3,1] | B. | [-1,3] | C. | (-∞,1] | D. | [3,+∞) |
2.将函数y=sin(2x+$\frac{π}{6}$)的图象向右平移$\frac{π}{6}$个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是( )
| A. | y=sin4x | B. | y=sinx | C. | y=sin(4x-$\frac{π}{6}$) | D. | y=sin(x-$\frac{π}{6}$) |
 在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,且PA⊥平面ABCD,点M是棱PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,且PA⊥平面ABCD,点M是棱PA的中点.