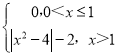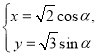题目内容
【题目】设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,则( )
,则( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
【答案】A
【解析】
当![]() 时,
时,![]() ,即
,即![]() ,则
,则![]() ,设
,设![]() 利用导数研究出函数
利用导数研究出函数![]() 的的单调性,从而得到
的的单调性,从而得到![]() ,即
,即![]() ,得到数列
,得到数列![]() 单调递增,则选项A正确,B错误,当
单调递增,则选项A正确,B错误,当![]() 时,
时,![]() ,即
,即![]() ,则
,则![]() ,设
,设![]() ,利用导数研究出函数
,利用导数研究出函数![]() 的的单调性,可得一定存在
的的单调性,可得一定存在![]() ,使得
,使得![]() ,
,![]() ,使得
,使得![]() ,当
,当![]() (或
(或![]() )时有,
)时有,![]() ,从而选项C, D不正确.
,从而选项C, D不正确.
当![]() 时,
时,![]() ,即
,即![]() .
.
则![]() ,设
,设![]() ,则
,则![]()
![]() ,所以
,所以![]() 在
在![]() 上单调递增,且
上单调递增,且![]()
所以当![]() 时,
时,![]() ,则
,则![]() 单调递增.
单调递增.
当![]() 时,
时,![]() ,则
,则![]() 单调递减.
单调递减.
所以![]() ,所以
,所以![]()
所以当![]() 时,数列
时,数列![]() 单调递增,则选项A正确,B错误.
单调递增,则选项A正确,B错误.
当![]() 时,
时,![]() ,即
,即![]() .
.
则![]() ,设
,设![]() ,则
,则![]()
![]() ,所以
,所以![]() 在
在![]() 上单调递增,且
上单调递增,且![]()
所以当![]() 时,
时,![]() ,则
,则![]() 单调递增.
单调递增.
当![]() 时,
时,![]() ,则
,则![]() 单调递减.
单调递减.
所以![]() ,又
,又![]() ,
,![]()
所以一定存在![]() ,使得
,使得![]() ,
,![]() ,使得
,使得![]()
当![]() (或
(或![]() )时有,
)时有,![]() ,即
,即![]() .
.
同理可得![]() ,
,![]() ,所以选项C, D不正确.
,所以选项C, D不正确.
故选:A

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目