题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(2)若存在![]() ,使得
,使得![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)
上单调递增;(2)![]() .
.
【解析】
(1)先对函数![]() 求导,然后根据
求导,然后根据![]() 的正负以及定义域,分类讨论
的正负以及定义域,分类讨论![]() 在
在![]() 上的单调性;
上的单调性;
(2)对![]() 分类:
分类:![]() ,
,![]() ,
,![]() ,考虑每种情况下
,考虑每种情况下![]() 所满足的不等式,并通过统一变量
所满足的不等式,并通过统一变量![]() 构造新函数
构造新函数![]() 分析并求解出
分析并求解出![]() 的最大值.
的最大值.
(1)![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 函数
函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() .
.
①当![]() 时,
时,![]()
![]() 时,
时,![]()
![]() 函数
函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() 为减函数,
为减函数,
![]() 时,
时,![]() 为增函数;
为增函数;
综上可知,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增.
上单调递增.
(2)当![]() 时,由
时,由![]() ,得
,得![]() 对
对![]() 恒成立.
恒成立.
因为函数![]() 在
在![]() 上单调递减,不能使
上单调递减,不能使![]() 对
对![]() 恒成立;
恒成立;
当![]() 时,
时,![]() ;
;
当![]() 时,由
时,由![]() ,
,
得![]() ,
,
设函数![]()
则![]()
令![]() ,可得
,可得![]() ,
,
![]() 时,
时,![]() 为减函数,
为减函数,
![]() 时,
时,![]() 为增函数.
为增函数.
![]() .
.
设![]()
![]() ,解得
,解得![]()
当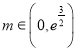 时,
时,![]() 为增函数,
为增函数,
当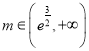 时,
时,![]() 为减函数.
为减函数.
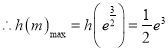
![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了![]() 人,将调查情况进行整理后制成下表:
人,将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(![]() )完成被调查人员的频率分布直方图.
)完成被调查人员的频率分布直方图.
(![]() )若从年龄在
)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行追踪调查,求恰有
人进行追踪调查,求恰有![]() 人不赞成的概率.
人不赞成的概率.
(![]() )在
)在![]() 在条件下,再记选中的
在条件下,再记选中的![]() 人中不赞成“车辆限行”的人数为
人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.