题目内容
(本小题满分12分)
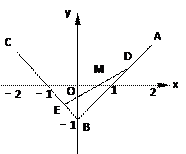
如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足="t," =" t" ,
="t" , t∈[0,1].
(Ⅰ) 求动直线DE斜率的变化范围;
(Ⅱ) 求动点M的轨迹方程.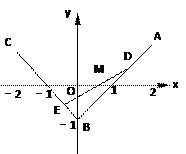
如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足="t," =" t" ,
="t" , t∈[0,1].
(Ⅰ) 求动直线DE斜率的变化范围;
(Ⅱ) 求动点M的轨迹方程.

(Ⅰ) kDE∈[-1,1].
(Ⅱ) 所求轨迹方程为: x2=4y, x∈[-2,2]
(Ⅱ) 所求轨迹方程为: x2=4y, x∈[-2,2]
解法一: 如图, (Ⅰ)设D(x0,y0),E(xE,yE),M(x,y).由=t,
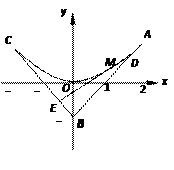
= t, 知(xD-2,yD-1)=t(-2,-2).
∴ 同理 .
∴kDE = = = 1-2t.
∵ t∈[0,1] , ∴kDE∈[-1,1].
t∈[0,1] , ∴kDE∈[-1,1].
(Ⅱ) ∵=t ∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)
=t(-2,4t-2)=(- 2t,4t2-2t).
2t,4t2-2t).
∴ , ∴y=, 即x2=4y.∵t∈[0,1], x=2(1-2t)∈[-2,2].
即所求轨迹方程为: x2=4y, x∈[-2,2]
解法二: (Ⅰ)同上.
(Ⅰ)同上.
(Ⅱ) 如图, ="+" =" + " t =" +" t(-) = (1-t) +t,
=" +" = +t = +t(-) =(1-t) +t,
=" +=" + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2.
设M点的坐标为(x,y),由=(2,1), =(0,-1), =( -2,1)得
-2,1)得
消去t得x2=4y
∵t∈[0,1], x∈[-2,2].
故所求轨迹方程为: x2=4y, x∈[-2,2]

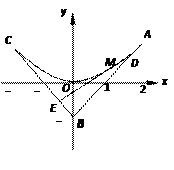
= t, 知(xD-2,yD-1)=t(-2,-2).
∴ 同理 .
∴kDE = = = 1-2t.
∵
 t∈[0,1] , ∴kDE∈[-1,1].
t∈[0,1] , ∴kDE∈[-1,1].(Ⅱ) ∵=t ∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)
=t(-2,4t-2)=(-
 2t,4t2-2t).
2t,4t2-2t). ∴ , ∴y=, 即x2=4y.∵t∈[0,1], x=2(1-2t)∈[-2,2].
即所求轨迹方程为: x2=4y, x∈[-2,2]
解法二:
 (Ⅰ)同上.
(Ⅰ)同上.(Ⅱ) 如图, ="+" =" + " t =" +" t(-) = (1-t) +t,
=" +" = +t = +t(-) =(1-t) +t,
=" +=" + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2.
设M点的坐标为(x,y),由=(2,1), =(0,-1), =(
 -2,1)得
-2,1)得消去t得x2=4y
∵t∈[0,1], x∈[-2,2].
故所求轨迹方程为: x2=4y, x∈[-2,2]

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
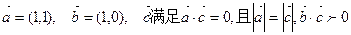
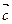 ;
;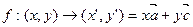
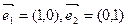 ,今有动点P从
,今有动点P从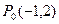 开始沿着与向量
开始沿着与向量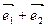 相同方向做匀速直线运动,速度为︱
相同方向做匀速直线运动,速度为︱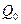 (-2,-
(-2,- 1)出发,沿着与向量
1)出发,沿着与向量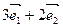 相同的方向做匀速直线运动,速度为︱
相同的方向做匀速直线运动,速度为︱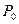 、
、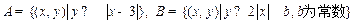 ,
,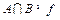 .
.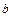 的取值范围是 ;
的取值范围是 ;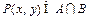 ,点
,点 的坐标为
的坐标为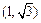 ,若
,若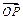 在
在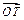 方向上投影的最小值为
方向上投影的最小值为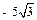 ,则
,则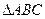 的三个内角
的三个内角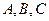 所对边的长分别为
所对边的长分别为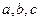 ,设向量
,设向量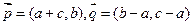
 .若
.若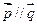 ,则角
,则角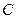 的大小为( )
的大小为( )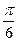
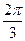
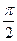

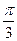
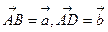 ,用a,b表示
,用a,b表示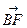 和
和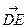 。
。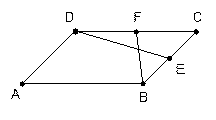
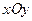 中,四边形
中,四边形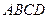 中,
中,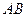 ∥
∥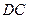 ,
,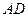 ∥
∥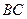 .已知点
.已知点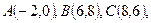 则
则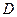 点的坐标为__
点的坐标为__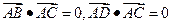 ,
,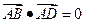 ,则
,则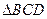 是
是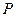 是
是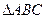 的外心,且
的外心,且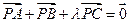 ,
,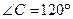 ,则实数
,则实数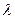 的值为( )
的值为( )