Question

【题目】已知椭圆 经过点 ，且离心率为 ．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设A，B是椭圆C的左，右顶点，P为椭圆上异于A，B的一点，以原点O为端点分别作与直线AP和BP平行的射线，交椭圆C于M，N两点，求证：△OMN的面积为定值．

Answer 1

【答案】解：（Ⅰ）∵椭圆 经过点 ，且离心率为 ，
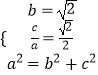∴ ，解得a=2，b= ，
∴椭圆C的方程为 ．
证明：（Ⅱ）设P（x0 ， y0），M（x1 ， y1），N（x2 ， y2），
①M（x1 ， y1），N（x2 ， y2）在x轴同侧，不妨设x1＞0，x2＜0，y1＞0，y2＞0，
射线OM的方程为y= ，射线ON的方程为y= ，
∴ ， ，且 ，
过M，N作x轴的垂线，垂足分别为M′，N′，
﹣
=
=
= = =﹣ ，
由 ，得 ，
即 = =2+x0 ，
同理， =2﹣x0 ， ∴ =4﹣ =2 ，即 ，
∴ ．
②M（x1 ， y1），N（x2 ， y2）在x轴异侧，同理①得 ，
综合①②，△OMN的面积为定值
【解析】（Ⅰ）由椭圆经过点 ，且离心率为 ，列出方程给求出a，b，由此能求出椭圆C的方程．（Ⅱ）设P（x0 ， y0），M（x1 ， y1），N（x2 ， y2），当M（x1 ， y1），N（x2 ， y2）在x轴同侧，不妨设x1＞0，x2＜0，y1＞0，y2＞0，推导出 ， ，且 ，过M，N作x轴的垂线，垂足分别为M′，N′， ﹣ =﹣ ，由 ，得 ，由此求出 ．当M（x1 ， y1），N（x2 ， y2）在x轴异侧，同理得 ，由此能证明△OMN的面积为定值 ．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．