题目内容
【题目】在单调递增数列{an}中,a1=2,a2=4,且a2n﹣1 , a2n , a2n+1成等差数列,a2n , a2n+1 , a2n+2成等比数列,n=1,2,3,….
(Ⅰ)(ⅰ)求证:数列 ![]() 为等差数列;
为等差数列;
(ⅱ)求数列{an}的通项公式.
(Ⅱ)设数列 ![]() 的前n项和为Sn , 证明:Sn>
的前n项和为Sn , 证明:Sn> ![]() ,n∈N* .
,n∈N* .
【答案】(Ⅰ)(ⅰ)证明:因为数列{an}为单调递增数列,a1=2>0,所以an>0(n∈N*).
由题意得2a2n=a2n﹣1+a2n+1 , ![]() ,
,
于是 ![]()
![]() ,
,
化简得 ![]() ,
,
所以数列 ![]() 为等差数列.
为等差数列.
(ⅱ)解:因为a3=2a2﹣a1=6, ![]() ,
,
所以数列 ![]() 的首项为
的首项为 ![]() ,公差为
,公差为 ![]() ,
,
所以 ![]() ,从而
,从而 ![]() .
.
结合 ![]() ,可得a2n﹣1=n(n+1).
,可得a2n﹣1=n(n+1).
因此,当n为偶数时an= ![]() ,当n为奇数时an=
,当n为奇数时an= ![]() .
.
2)证明:通过(ii)可知 ![]() =
= ![]() .
.
因为an= ![]() ,
,
所以 ![]() ,
,
∴ ![]() +…
+… ![]()
![]()
= ![]() ,
,
所以Sn> ![]() ,n∈N*
,n∈N*
【解析】(Ⅰ)(ⅰ)通过题意可知2a2n=a2n﹣1+a2n+1、 ![]() ,化简即得结论;(ⅱ)通过计算可知数列
,化简即得结论;(ⅱ)通过计算可知数列 ![]() 的首项及公差,进而可得结论;(2)通过(ii)、放缩、裂项可知
的首项及公差,进而可得结论;(2)通过(ii)、放缩、裂项可知 ![]() >4(
>4( ![]() ﹣
﹣ ![]() ),进而并项相加即得结论.
),进而并项相加即得结论.
【考点精析】掌握等差关系的确定和数列的前n项和是解答本题的根本,需要知道如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系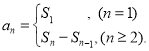 .
.

练习册系列答案
相关题目