题目内容
7.在△ABC中a2+b2=$\frac{1}{2}$c2,则直线ax-by+c=0被圆x2+y2=9所截得的弦长为2$\sqrt{7}$.分析 求出圆心(0,0)到直线ax-by+c=0的距离d,再利用弦长公式求得弦长.
解答 解:由题意得圆心(0,0)到直线ax-by+c=0的距离等于d=$\frac{|c|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{2}$,
由弦长公式得弦长等于2$\sqrt{9-2}$=2$\sqrt{7}$,
故答案为:2$\sqrt{7}$.
点评 本题考查点到直线的距离公式、弦长公式的应用,求出圆心(0,0)到直线ax-by+c=0的距离是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知随机变量X服从正态分布,其正态分布密度曲线为函数f(x)=$\frac{1}{\sqrt{2π}}$e${\;}^{\frac{-(x-2)^{2}}{2}}$的图象,若${∫}_{0}^{2}$f(x)dx=$\frac{1}{3}$,则P(X>4)=( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
16.若$θ∈[{\frac{π}{4},\frac{π}{2}}]$,$sin2θ=\frac{{4\sqrt{2}}}{9}$,则sinθ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
17.执行如图所示的程序框图,若a=9,b=1,则输出的结果是( )
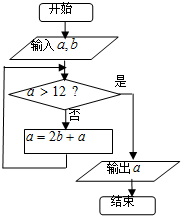

| A. | 9 | B. | 11 | C. | 13 | D. | 15 |
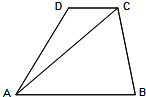 在梯形ABCD中,AB∥CD,CD=2,∠ADC=120°,cos$∠CAD=\frac{5\sqrt{7}}{14}$
在梯形ABCD中,AB∥CD,CD=2,∠ADC=120°,cos$∠CAD=\frac{5\sqrt{7}}{14}$