题目内容

12．已知{an}为等差数列，Sn为其前n项和．若a3=-6，S1=S5，则公差d=12；Sn的最小值为-54．

分析 通过设数列{an}的公差为d，利用S1=S5即a2+a3+a4+a5=0可知-24+2d=0，进而可得结论．

解答 解：设数列{an}的公差为d，
∵a3=-6，
∴a2=-6-d，a4=-6+d，a5=-6+2d，
又∵S1=S5，
∴a2+a3+a4+a5=0，即-24+2d=0，
解得：d=12，
∴a1=a3-2d=-6-24=-30，∴an=-30+12（n-1）=12n-42，
∴Sn=$\frac{n（-30+12n-42）}{2}$=6（n-3）2-54，
∴当n=3时Sn取最小值-54，
故答案为：12；-54．

点评 本题考查数列的通项及前n项和，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
2．在锐角△ABC中，角A，B，C的对边分别是a，b，c，若A=2B，则$\frac{c}{b}$的取值范围是（　　）
A．（1，3）B．（2，3）C．（0，3）D．（1，2）
3．在△ABC中，$\frac{π}{3}$≤B≤$\frac{π}{2}$，求证：a+c≤2b．
20．已知函数f（x）=|x+1|-|x|+a．
（1）若a=0，求不等式f（x）≥0的解集；
（2）若不等式f（x）≥0的解集为R，求A的取值范围．
7．在△ABC中a2+b2=$\frac{1}{2}$c2，则直线ax-by+c=0被圆x2+y2=9所截得的弦长为2$\sqrt{7}$．
17．执行如图所示的程序框图，则输出的T值为（　　）
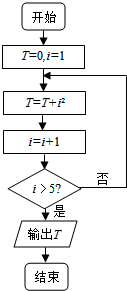
A．30B．54C．55D．91
4．命题“若x＞1，则x2＞x“的否命题为x≤1，则x2≤x．
1．设数列{an}满足a1=0，${a_{n+1}}=\frac{1}{{b-{a_n}}}$，n∈N*．
（1）若b=2，求数列{an}的通项公式；
（2）令${c_n}=\frac{{{a_n}-p}}{{p{a_n}-1}}$（其中常数p＞0，且p≠1），若{cn}是等比数列，求实数b的取值范围．
2．在下列各题中，p是q的什么条件？
（1）p：x2=3x+4；，q：x=$\sqrt{3x+4}$；
（2）p：x-3=0，q：（x-3）（x-4）=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网