��Ŀ����
����Ŀ��ij����Ϊ�˹涨��ʱ����,��Ҫȷ���ӹ���������ѵ�ʱ��,Ϊ�˽�����5������,�ռ��������±�:
�ӹ��������x/�� | 10 | 20 | 30 | 40 | 50 |
�ӹ�ʱ��y/���� | 64 | 69 | 75 | 82 | 90 |
������,�����������ݾ���������ع�ϵ,��ô���ڼӹ�����ĸ���x��ӹ�ʱ��y����������,�����ж���ȷ����(����)
A. �������,��ع�ֱ�߾�����(30,75)
B. �������,��ع�ֱ�߾�����(30,76)
C. �ɸ����,��ع�ֱ�߾�����(30,76)
D. �ɸ����,��ع�ֱ�߾�����(30,75)
���𰸡�B
��������������������ݱ������������ݣ��õ�������Ϊ����أ���������ݱ��ƽ�������õ��������ĵ㣬�����õ����ۣ�
�⣺�ɱ�������֪���ӹ�ʱ����ӹ�����ĸ��������Ӷ����ӣ���������Ϊ����أ�
����![]() =30��
=30��![]() =
=![]() ��64+69+75+82+90��=76��
��64+69+75+82+90��=76��
�ʻع�ֱ�߹��������ĵ㣨30��76����
��ѡ��B��

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
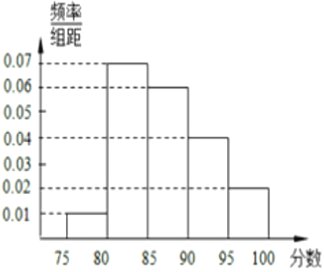
�����ҵ�����������ѧ���ӳ�����ϵ�д�����Ŀ��ij��У�ڽ���������������Գɼ��������ȡ 100 �������ı��Գɼ�����Ϊ 5 ���Ƴ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
��� | ���� | Ƶ�� | Ƶ�� |
1 |
| 5 | 0.05 |
2 |
| 35 | 0.35 |
3 |
|
|
|
4 |
|
|
|
5 |
| 10 | 0.1 |
(1)��![]() ��ֵ.
��ֵ.
(2)��У�����ڳɼ��Ϻõ� ��4��5 ���÷ֲ������ȡ 6 ��ѧ���������ԣ���ÿ��Ӧ���������ѧ����
(3)��(2)��ǰ���£��ӳ鵽 6 ��ѧ�����������ȡ 2 �����������ԣ����� 2 ��ѧ������ͬһ��ĸ���.