题目内容
11.已知cos2α=$\frac{4}{5}$,且2α∈[π,2π],求sinα,cos4α.分析 由题意求出α的范围,根据二倍角的余弦公式的变形依次求出sinα,cos4α的值.
解答 解:∵cos2α=$\frac{4}{5}$>0,且2α∈[π,2π],
∴2α∈[$\frac{3π}{2}$,2π],则α∈[$\frac{3π}{4}$,π],
∴sinα=$\sqrt{\frac{1-cos2α}{2}}$=$\frac{\sqrt{10}}{10}$,
cos4α=2cos22α-1=$-\frac{7}{25}$.
点评 本题考查二倍角的余弦公式的变形的灵活应用,以及三角函数值的符号,注意角之间的关系,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
6.如图⊙O中,弦AB与弦CD相交于点P,∠B=38°,∠APD=80°,则∠A等于( )
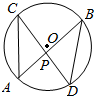

| A. | 38° | B. | 42° | C. | 80° | D. | 118° |
16.在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数.满分100分,按照大于等于80分为优秀,小于80分为合格.为了解学生在该维度的测评结果,从毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表.
下面的临界值表供参考:
已知在该班随机抽取1人测评结果为优秀的概率为$\frac{1}{3}$.
(1)请完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
| 优秀 | 合格 | 总计 | |
| 男生 | 6 | ||
| 女生 | 18 | ||
| 总计 | 60 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)请完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
3.设(x+3)(2x+3)10=a0+a1(x+3)+a2(x+3)2+…+a11(x+3)11,则a0+a1+a2+…+a11的值为( )
| A. | 1 | B. | 2 | C. | 311 | D. | 4×510 |
20.下列说法正确的是( )
| A. | 如果两个复数的实部的差和虚部的差都等于0,那么这两个复数相等 | |
| B. | ai是纯虚数(a∈R) | |
| C. | 如果复数x+yi(x,y∈R)是实数,则x=0,y=0 | |
| D. | 复数a+bi(a,b∈R)不是实数 |
1.记anan-1…a1a0(k)) 表示一个k进制数,若21(k)=9(10),则321(k)在十进制中所表示的数为( )
| A. | 86 | B. | 57 | C. | 34 | D. | 17 |