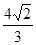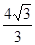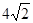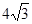题目内容
已知圆柱M的底面圆的半径与球O的半径相同,若圆柱M与球O的表面积相等,则它们的体积之比 .(用数值作答)
.(用数值作答)
 .(用数值作答)
.(用数值作答)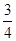
解:∵设圆柱M的底面圆的半径与球O的半径均为R,M的高为h
则球的表面积S球=4πR2又∵圆柱M与球O的表面积相等即4πR2=2πR2+2πR•h
解得h=R则V圆柱=πR3,V球="4" /3 πR3∴V圆柱:V球="3/" 4故答案为:3 /4
则球的表面积S球=4πR2又∵圆柱M与球O的表面积相等即4πR2=2πR2+2πR•h
解得h=R则V圆柱=πR3,V球="4" /3 πR3∴V圆柱:V球="3/" 4故答案为:3 /4

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
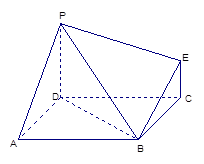
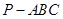 中,
中,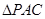 和
和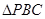 是边长为
是边长为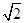 的等边三角形,
的等边三角形,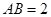 ,
,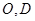 分别是
分别是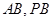 的中点.
的中点.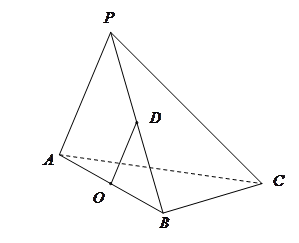
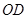 ∥平面
∥平面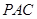 ;
;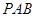 ⊥平面
⊥平面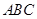 ;
;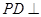 平面
平面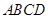 ,
,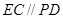 ,且
,且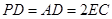 ="2" .
="2" .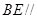 平面
平面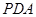 ;
;
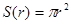 ,周长
,周长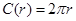 ,若将
,若将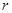 看作是
看作是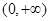 上的变量,则
上的变量,则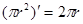 ……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为
……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为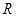 的球,若将
的球,若将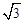 正方形。若PA=2
正方形。若PA=2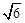 ,则△OAB的面积为______________.
,则△OAB的面积为______________.
 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个鸡蛋蛋巢,将表面积为4
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个鸡蛋蛋巢,将表面积为4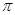 的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与鸡蛋巢底面的距离为___________.
的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与鸡蛋巢底面的距离为___________.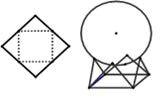
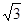 ,则这个正四棱锥的体积是( )
,则这个正四棱锥的体积是( )