题目内容
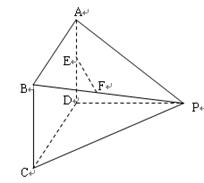
在三棱锥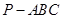 中,
中,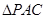 和
和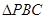 是边长为
是边长为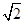 的等边三角形,
的等边三角形,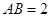 ,
,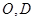 分别是
分别是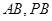 的中点.
的中点.
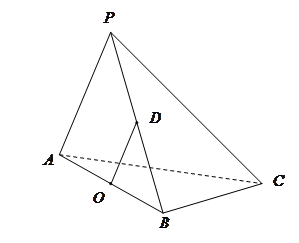
(Ⅰ)求证: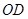 ∥平面
∥平面 ;
;
(Ⅱ)求证:平面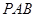 ⊥平面
⊥平面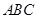 ;
;
(Ⅲ)求三棱锥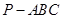 的体积.
的体积.
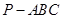 中,
中,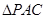 和
和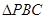 是边长为
是边长为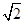 的等边三角形,
的等边三角形,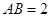 ,
,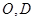 分别是
分别是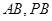 的中点.
的中点.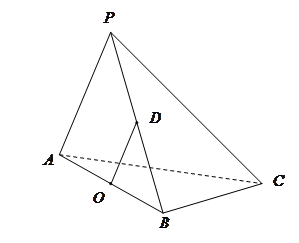
(Ⅰ)求证:
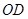 ∥平面
∥平面 ;
;(Ⅱ)求证:平面
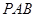 ⊥平面
⊥平面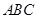 ;
;(Ⅲ)求三棱锥
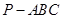 的体积.
的体积.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)

本题主要考查直线与平面平行的判定,以及平面与平面垂直的判定和三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.
(1)欲证OD∥平面PAC,根据直线与平面平行的判定定理可知只需证OD与平面PAC内一直线平行,而OD∥PA,PA?平面PAC,OD?平面PAC,满足定理条件;
(2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.
解:(Ⅰ) 分别为
分别为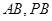 的中点,
的中点,

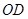 ∥
∥
又 平面
平面 ,
, 平面
平面
 ∥平面
∥平面 . ………………5分
. ………………5分
(Ⅱ)连结 ,
,
 ,
, 为
为 中点,
中点,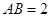 ,
,
 ⊥
⊥ ,
, .
.
同理, ⊥
⊥ ,
, .
.
又 ,
, ,
,
 ,
, ⊥
⊥ .
.

 ⊥
⊥ ,
, ⊥
⊥ ,
, ,
,
 ⊥平面
⊥平面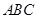 .
.
又
 平面
平面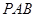 ,
, 平面
平面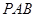 ⊥平面
⊥平面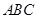 .…………………10分
.…………………10分
(Ⅲ)由(Ⅱ)可知 垂直平面
垂直平面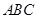

 为三棱锥
为三棱锥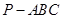 的高,且
的高,且
 . …………………………14分
. …………………………14分
(1)欲证OD∥平面PAC,根据直线与平面平行的判定定理可知只需证OD与平面PAC内一直线平行,而OD∥PA,PA?平面PAC,OD?平面PAC,满足定理条件;
(2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.
解:(Ⅰ)
 分别为
分别为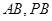 的中点,
的中点,
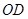 ∥
∥
又
 平面
平面 ,
, 平面
平面
 ∥平面
∥平面 . ………………5分
. ………………5分(Ⅱ)连结
 ,
,
 ,
, 为
为 中点,
中点,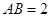 ,
, ⊥
⊥ ,
, .
.同理,
 ⊥
⊥ ,
, .
.又
 ,
, ,
, ,
, ⊥
⊥ .
.
 ⊥
⊥ ,
, ⊥
⊥ ,
, ,
, ⊥平面
⊥平面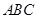 .
.又

 平面
平面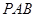 ,
, 平面
平面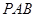 ⊥平面
⊥平面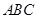 .…………………10分
.…………………10分(Ⅲ)由(Ⅱ)可知
 垂直平面
垂直平面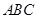

 为三棱锥
为三棱锥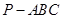 的高,且
的高,且
 . …………………………14分
. …………………………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
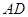 ⊥平面
⊥平面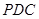 ,
,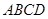 为平行四边形,
为平行四边形,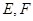 分别为
分别为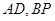 的中点,
的中点,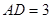 ,
,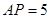 ,
,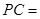
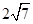 .
.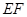 ∥平面
∥平面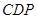 =90°,求证
=90°,求证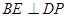 ;
;
 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
 ⊥平面
⊥平面 ;
; ⊥平面
⊥平面 ,求三棱锥
,求三棱锥 的体积.
的体积. 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,点
,点 是
是 的中点.
的中点.
 //平面
//平面 ;
; 的体积为
的体积为 ,求
,求 的长.
的长. ,则
,则 的取值范围为
的取值范围为
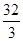 π,那么这个三棱柱的体积是( )
π,那么这个三棱柱的体积是( )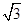
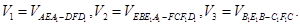 若
若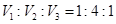 ,则截面
,则截面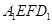 的面积为( )
的面积为( )
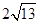 B.
B.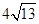
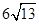 D.
D.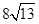
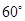 的二面角
的二面角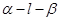 内一点,
内一点,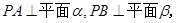
 垂足,
垂足,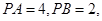 则AB的长为( )
则AB的长为( )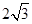
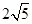
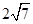
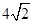
 .(用数值作答)
.(用数值作答)