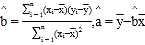题目内容
【题目】一些选手参加数学竞赛，其中有些选手互相认识，有些选手互相不认识，而任何两个不相识的选手都恰有两个共同的熟人．若
与
认识，但没有共同的熟人，求证：、认识的熟人一样多．
【答案】见解析
【解析】
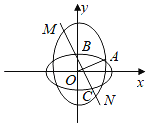
用点表示人，两人互相认识就在相应两点间连一条线段，依题意
间有连线（如图）．
由于
、
没有共同的熟人，故凡认识的人就不认识，凡认识的人就不认识．
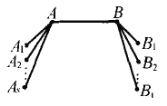
现设
，
，…，
与认识，
，
，…，
与认识，由于任一
与不认识，而任何两个不相识的选手都恰有两个共同的熟人，故
与有且仅有一个共同的熟人
．
反之，每一个
与有且仅有一个共同的熟人．
亦即每一必与某一有连线，每一也必与某一
有连线．
现设
与
认识，
与
认识，下面证明与不相同时，与也不相同．
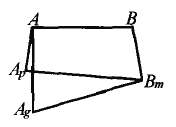
若不然，与重合，则、与均有连线，从而互不认识的，共同认识3个人，，（如图），与已知条件“恰有两个共同的熟人”矛盾，可见，
．
同理，，不相同时，其对应的，也不相同，又得
．
从而
．这表明、认识的熟人一样多．
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案【题目】如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
（1）请画出表中数据的散点图；
（2）请根据表中提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（3）根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗多少吨标准煤？
（附：
，
）
【题目】为了提高学生的身体素质，某校高一、高二两个年级共
名学生同时参与了“我运动，我健康，我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况，采用分层抽样的方法从高一、高二两个年级的学生中分别抽取
名和
名学生进行测试.下表是高二年级的名学生的测试数据（单位：个/分钟）：
学生编号 | 1 | 2 | 3 | 4 | 5 |
跳绳个数 | 179 | 181 | 168 | 177 | 183 |
踢毽个数 | 85 | 78 | 79 | 72 | 80 |
（1）求高一、高二两个年级各有多少人？
（2）设某学生跳绳
个/分钟，踢毽
个/分钟.当
，且
时，称该学生为“运动达人”.
①从高二年级的学生中任选一人，试估计该学生为“运动达人”的概率；
②从高二年级抽出的上述名学生中，随机抽取
人，求抽取的名学生中为“span>运动达人”的人数
的分布列和数学期望.
