题目内容
【题目】如图,椭圆W:![]() 的焦距与椭圆Ω:
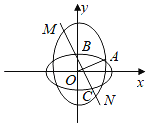
的焦距与椭圆Ω:![]() +y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
+y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
(1)求W的标准方程:
(2)求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得![]() ,求出a2,b2,即可得到W的标准方程,
,求出a2,b2,即可得到W的标准方程,
(2)先求出直线l的方程为y=﹣3x+1,分别与椭圆W和椭圆Ω,联立方程组,求出BC和MN,比较即可
(1)由题意可得![]() ,
,
∴![]()
故W的标准方程为![]() .
.
(2)联立 得
得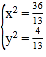
∴![]() ,
,
∴![]() ,
,
易知B(0,1),
∴l的方程为y=﹣3x+1.
联立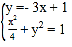 ,得37x2﹣24x=0,
,得37x2﹣24x=0,
∴x=0或![]() ,
,
∴![]() ,
,
联立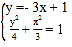 ,得31x2﹣18x﹣9=0,
,得31x2﹣18x﹣9=0,
设M(x1,y1),N(x2,y2),
则![]() ,
,![]() ,
,
∴![]() ,
,
故![]() .
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
【题目】某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理.
(Ⅰ)若小店一天购进16份,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)小店一天购进16份这种食品,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份?

