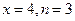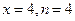题目内容
若(x-1)4=a0+a1x+a2x2+a3x3+a4x4,则a0+a2+a4的值为______.
∵(x-1)4=(1-x)4=
+
(-x)+
•(-x)2+
•(-x)3+
•(-x)4,
∴a0+a2+a4 =
+
+
=1+6+1=8,
故答案为 8.
| C | 04 |
| C | 14 |
| C | 24 |
| C | 34 |
| C | 44 |
∴a0+a2+a4 =
| C | 04 |
| C | 24 |
| C | 44 |
故答案为 8.

练习册系列答案
相关题目
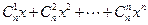 能被
能被 整除,则
整除,则 的值可能为 ( )
的值可能为 ( )