题目内容
设函数f(x)=sin(2x+
),现有下列结论:
(1)f(x)的图象关于直线x=
对称;
(2)f(x)的图象关于点(
,0)对称
(3)把f(x)的图象向左平移
个单位,得到一个偶函数的图象;
(4)f(x)的最小正周期为π,且在[0,
]上为增函数.
其中正确的结论有______(把你认为正确的序号都填上)
| π |
| 3 |
(1)f(x)的图象关于直线x=
| π |
| 3 |
(2)f(x)的图象关于点(
| π |
| 4 |
(3)把f(x)的图象向左平移
| π |
| 12 |
(4)f(x)的最小正周期为π,且在[0,
| π |
| 6 |
其中正确的结论有______(把你认为正确的序号都填上)
根据正弦函数的性质可知f(x)=sin(2x+
)的对称轴为2x+
=kπ+
(k∈Z),即x=
+
(k∈Z)∴直线x=
不是函数f(x)的对称轴,结论(1)错误
根据正弦函数的性质可知f(x)=sin(2x+
)的对称中心横坐标为2x+
=kπ,即x=
-
,∴点(
,0)不是函数的对称中心.结论(2)错误.
f(x)的图象向左平移
个单位,得f(x)=sin(2x+
)=cos2x,为偶函数,∴结论(3)正确.
f(x)的最小正周期为π,且2kπ-
≤2x+
≤2kπ+
时,即kπ-
π≤x≤kπ+
函数单调增,∴结论(4)不正确.
故答案为(3)
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
| π |
| 3 |
根据正弦函数的性质可知f(x)=sin(2x+
| π |
| 3 |
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
| π |
| 4 |
f(x)的图象向左平移
| π |
| 12 |
| π |
| 2 |
f(x)的最小正周期为π,且2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5 |
| 6 |
| π |
| 12 |
故答案为(3)

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
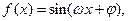 其中
其中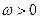 ,
,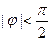 ,
,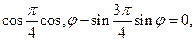 求
求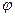 的值;
的值; 

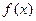 的图象的相邻两条对称轴之间的距离等于
的图象的相邻两条对称轴之间的距离等于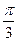 ,求函数
,求函数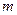 ,使得函数
,使得函数 的定义域为
的定义域为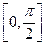 ,值域为
,值域为 .试求函数
.试求函数 (
(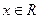 )的最小正周期和最值.
)的最小正周期和最值.