题目内容
(本小题满分14分)
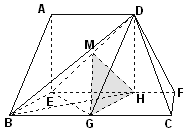
在如图所示的多面体中,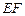 ⊥平面
⊥平面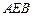 ,
, 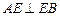 ,
,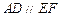 ,
,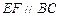 ,
,
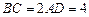 ,
,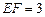 ,
,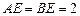 ,
,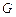 是
是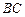 的中点.
的中点.
(1)求证: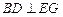 ;
;
(2)求平面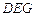 与平面
与平面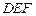 所成锐二面角的余弦值.
所成锐二面角的余弦值.
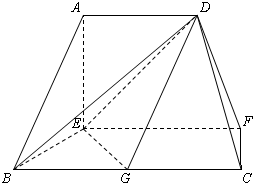
在如图所示的多面体中,
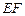 ⊥平面
⊥平面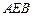 ,
, 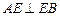 ,
,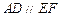 ,
,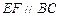 ,
,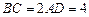 ,
,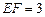 ,
,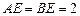 ,
,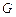 是
是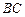 的中点.
的中点.(1)求证:
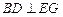 ;
;(2)求平面
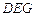 与平面
与平面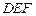 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1) 解法1
证明:∵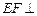 平面
平面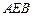 ,
,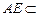 平面
平面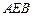 ,
,
∴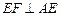 ,
,
又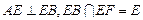 ,
,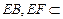 平面
平面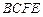 ,
,
∴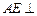 平面
平面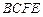 . …………2分
. …………2分
过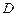 作
作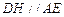 交
交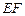 于
于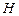 ,则
,则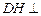 平面
平面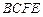 .
.
∵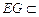 平面
平面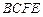 ,
,
∴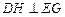 . …………4分
. …………4分
∵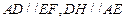 ,∴四边形
,∴四边形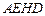 平行四边形,
平行四边形,
∴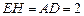 ,
,
∴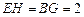 ,又
,又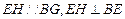 ,
,
∴四边形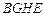 为正方形,
为正方形,
∴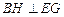 , ……………6分
, ……………6分
又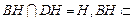 平面
平面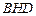 ,
,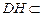 平面
平面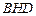 ,
,
∴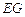 ⊥平面
⊥平面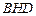 . ………………………7分
. ………………………7分
∵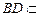 平面
平面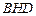 ,
,
∴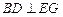 . ………………………8分
. ………………………8分
(2)∵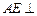 平面
平面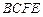 ,
,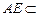 平面
平面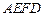
∴平面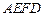 ⊥平面
⊥平面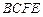
由(1)可知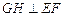
∴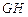 ⊥平面
⊥平面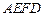
∵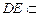 平面
平面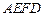
∴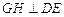 ……………………9分
……………………9分
取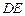 的中点
的中点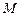 ,连结
,连结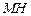 ,
,
∵四边形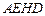 是正方形,
是正方形,
∴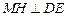
∵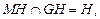
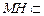 平面
平面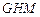 ,
,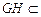 平面
平面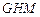
∴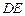 ⊥平面
⊥平面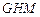
∴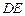 ⊥
⊥
∴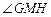 是二面角
是二面角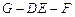 的平面角, ………………………12分
的平面角, ………………………12分
由计算得
∴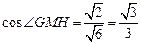 ………………………13分
………………………13分
∴平面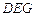 与平面
与平面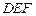 所成锐二面角的余弦值为
所成锐二面角的余弦值为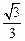 .………………………14分
.………………………14分
解法2
∵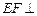 平面
平面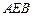 ,
,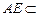 平面
平面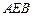 ,
,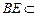 平面
平面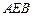 ,
,
∴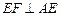 ,
,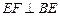 ,
,
又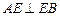 ,
,
∴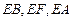 两两垂直. ……………………2分
两两垂直. ……………………2分
以点E为坐标原点,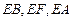 分别为
分别为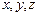 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
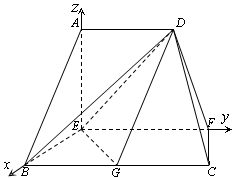
由已知得, (0,0,2),
(0,0,2),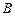 (2,0,0),
(2,0,0),
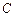 (2,4,0),
(2,4,0),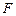 (0,3,0),
(0,3,0),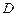 (0,2,2),
(0,2,2),
 (2,2,0). …………………………4分
(2,2,0). …………………………4分
∴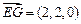 ,
,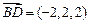 ,………6分
,………6分
∴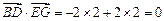 , ………7分
, ………7分
∴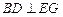 . …………………………8分
. …………………………8分
(2)由已知得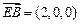 是平面
是平面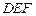 的法向量.
的法向量. ………………………9分
………………………9分
设平面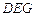 的法向量为
的法向量为 ,
,
∵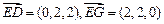 ,
,
∴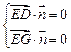 ,即
,即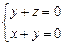 ,令
,令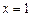 ,得
,得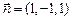 . ……………12分
. ……………12分
设平面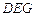 与平面
与平面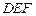 所成锐二面角的大小为
所成锐二面角的大小为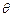 ,
,
则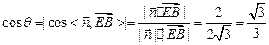 …………………………13分
…………………………13分
∴平面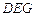 与平面
与平面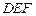 所成锐二面角的余弦值为
所成锐二面角的余弦值为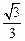 . …………………………14分
. …………………………14分

证明:∵
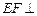 平面
平面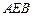 ,
,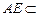 平面
平面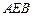 ,
,∴
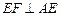 ,
, 又
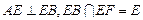 ,
,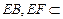 平面
平面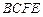 ,
,∴
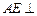 平面
平面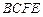 . …………2分
. …………2分过
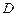 作
作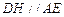 交
交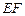 于
于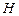 ,则
,则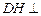 平面
平面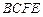 .
.∵
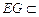 平面
平面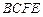 ,
, ∴
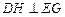 . …………4分
. …………4分∵
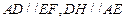 ,∴四边形
,∴四边形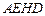 平行四边形,
平行四边形,∴
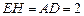 ,
,∴
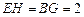 ,又
,又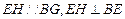 ,
,∴四边形
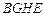 为正方形,
为正方形,∴
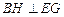 , ……………6分
, ……………6分又
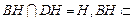 平面
平面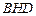 ,
,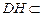 平面
平面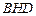 ,
,∴
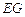 ⊥平面
⊥平面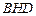 . ………………………7分
. ………………………7分∵
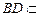 平面
平面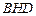 ,
,∴
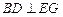 . ………………………8分
. ………………………8分(2)∵
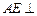 平面
平面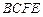 ,
,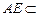 平面
平面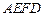
∴平面
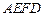 ⊥平面
⊥平面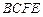
由(1)可知
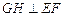
∴
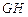 ⊥平面
⊥平面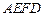
∵
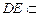 平面
平面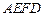
∴
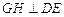 ……………………9分
……………………9分取
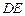 的中点
的中点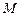 ,连结
,连结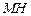 ,
,
∵四边形
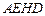 是正方形,
是正方形,∴
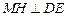
∵
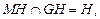
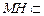 平面
平面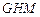 ,
,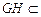 平面
平面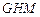
∴
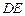 ⊥平面
⊥平面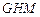
∴
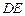 ⊥
⊥
∴
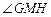 是二面角
是二面角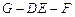 的平面角, ………………………12分
的平面角, ………………………12分由计算得

∴
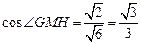 ………………………13分
………………………13分∴平面
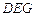 与平面
与平面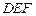 所成锐二面角的余弦值为
所成锐二面角的余弦值为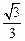 .………………………14分
.………………………14分解法2
∵
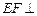 平面
平面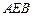 ,
,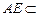 平面
平面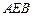 ,
,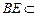 平面
平面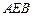 ,
,∴
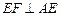 ,
,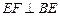 ,
,又
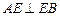 ,
,∴
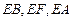 两两垂直. ……………………2分
两两垂直. ……………………2分以点E为坐标原点,
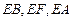 分别为
分别为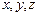 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
由已知得,
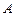 (0,0,2),
(0,0,2),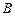 (2,0,0),
(2,0,0),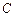 (2,4,0),
(2,4,0),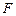 (0,3,0),
(0,3,0),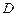 (0,2,2),
(0,2,2),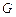 (2,2,0). …………………………4分
(2,2,0). …………………………4分∴
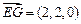 ,
,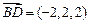 ,………6分
,………6分∴
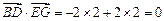 , ………7分
, ………7分∴
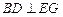 . …………………………8分
. …………………………8分(2)由已知得
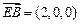 是平面
是平面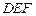 的法向量.
的法向量. ………………………9分
………………………9分设平面
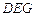 的法向量为
的法向量为 ,
,∵
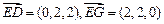 ,
,∴
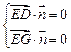 ,即
,即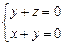 ,令
,令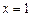 ,得
,得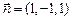 . ……………12分
. ……………12分设平面
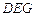 与平面
与平面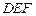 所成锐二面角的大小为
所成锐二面角的大小为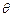 ,
,则
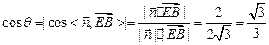 …………………………13分
…………………………13分∴平面
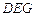 与平面
与平面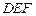 所成锐二面角的余弦值为
所成锐二面角的余弦值为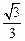 . …………………………14分
. …………………………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,如图E、F分别是
中,如图E、F分别是  ,CD的中点,
,CD的中点, 平面ADE;
平面ADE; .
. 
 中,则异面直线
中,则异面直线 与
与 所成的角是
所成的角是 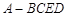 的底面
的底面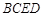 是直角梯形,
是直角梯形,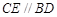 ,
,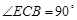 ,
,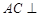 平面
平面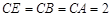 ,
,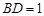 .
.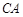 与平面
与平面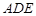 所成角的正弦值;
所成角的正弦值;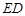 上是否存在一点
上是否存在一点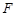 ,使得异面直线
,使得异面直线 与
与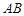 所成角余 弦值等
所成角余 弦值等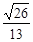 ?若存在,试确定点
?若存在,试确定点
 使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只
使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只

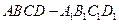 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).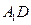 与直线
与直线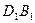 所成的角为 ▲ .
所成的角为 ▲ .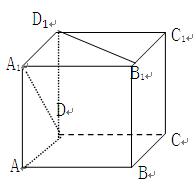
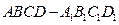 中,异面直线AC与
中,异面直线AC与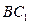 所成的角为 _____
所成的角为 _____ 点C在平面α外,AC和BC与平面α所成的角分别为300和450角,且平面ABC与平面α成600的锐二面角,则sin∠ACB=( )
点C在平面α外,AC和BC与平面α所成的角分别为300和450角,且平面ABC与平面α成600的锐二面角,则sin∠ACB=( ) 