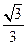题目内容
如图,在棱长为2的正方体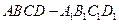 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
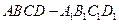 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).过E作EF⊥BC,交BC于F,连接DF.
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角.
由题意,得EF=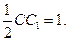
∵
∵ EF⊥DF, ∴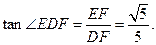
故直线DE与平面ABCD所成角的大小是
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角.
由题意,得EF=
∵

∵ EF⊥DF, ∴
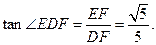
故直线DE与平面ABCD所成角的大小是

略

练习册系列答案
相关题目
 ⊥平面
⊥平面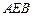 ,
, 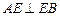 ,
,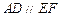 ,
,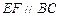 ,
,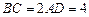 ,
,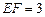 ,
,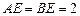 ,
, 是
是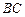 的中点.
的中点.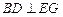 ;
;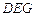 与平面
与平面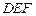 所成锐二面角的余弦值.
所成锐二面角的余弦值.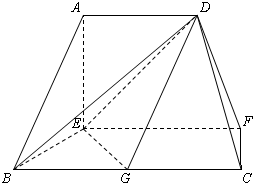
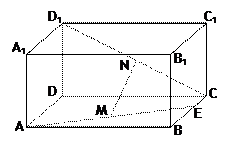
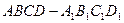 中,E是BC的中点,M、N分别是AE、
中,E是BC的中点,M、N分别是AE、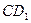 的中点,
的中点,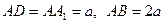 .
. 
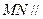 平面
平面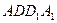
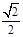





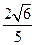


 ( )
( )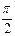

 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是 的中点,
的中点, 所成的角的余弦值为
所成的角的余弦值为