题目内容
【题目】若数列{an}是等差数列，首项a1＞0，a2003+a2004＞0，a2003 ． a2004＜0，则使前n项和Sn＞0成立的最大自然数n是（ ）
A.4005
B.4006
C.4007
D.4008
【答案】B
【解析】解：
解法1：由a2003+a2004＞0，a2003a2004＜0，知a2003和a2004两项中有一正数一负数，又a1＞0，则公差为负数，否则各项总为正数，故a2003＞a2004 ， 即a2003＞0，a2004＜0．
∴S4006= 
= 
＞0，
∴S4007= 
（a1+a4007）=4007a2004＜0，
故4006为Sn＞0的最大自然数．选B．
解法2：由a1＞0，a2003+a2004＞0，a2003a2004＜0，同解法1的分析得a2003＞0，a2004＜0，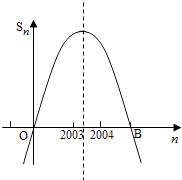 
∴S2003为Sn中的最大值．
∵Sn是关于n的二次函数，如草图所示，
∴2003到对称轴的距离比2004到对称轴的距离小，
∴ 在对称轴的右侧．
根据已知条件及图象的对称性可得4006在图象中右侧零点B的左侧，4007，4008都在其右侧，Sn＞0的最大自然数是4006．
对于首项大于零的递减的等差数列，第2003项与2004项的和大于零，积小于零，说明第2003项大于零且2004项小于零，且2003项的绝对值比2004项的要大，由等差数列前n项和公式可判断结论．
练习册系列答案
相关题目
