Question

【题目】某中学校本课程开设了A、B、C、D共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：

（Ⅰ）求这3名学生选修课所有选法的总数；

（Ⅱ）求恰有2门选修课没有被这3名学生选择的概率；

（Ⅲ）求A选修课被这3名学生选择的人数的分布列 .

Answer 1

【答案】（1）64.

（2）.

（3）见解析.

【解析】

（1）每个学生有四个不同的选择，由此根据分步乘法计数原理，能求出这3名学生选修课所有选法的总数．
（2）由已知利用排列组合知识能求出恰有2门选修课这3名学生都没选择的概率．
（3）A选修课被这3名学生选择的人数为，则的可能取值为0，1，2，3，分别求出相应的概率，由此能求出ξ的分布列．

(Ⅰ)每个学生有四个不同选择，根据乘法法则，选法总数N=

(Ⅱ) 恰有2门选修课这3名学生都没选择的概率为

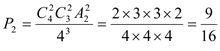
(Ⅲ) 设A选修课被这3名学生选择的人数为，则＝0,1,2,3

P(＝0)＝,　　 P(＝1)＝,

P(＝2)＝,　　 P(＝3)＝ ,

∴A选修课被这3名学生选择的人数的分布列为