题目内容
10.已知x与y之间的几组数据如下表:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | $\widehat{b}$>b,$\widehat{a}$>a | B. | $\widehat{b}$>b,$\widehat{a}$<a | C. | $\widehat{b}$<b,$\widehat{a}$>a | D. | $\widehat{b}$<b,$\widehat{a}$<a |
分析 利用数据求出回归直线方程$\hat y=\hat bx+\hat a$的系数,利用数据(4,3)和(5,4)求得的直线方程y=bx+a,比较可得结论.
解答 解:由题意可知n=4,$\overline{x}$=$\frac{3+4+5+6}{4}$=$\frac{9}{2}$=4.5,$\overline{y}$=$\frac{2.5+3+4+4.5}{4}$=$\frac{7}{2}$=3.5,
则$\widehat{b}$=$\frac{3×2.5+4×3+5×4+6×4.5-4×\frac{9}{2}×\frac{7}{2}}{{3}^{2}+{4}^{2}+{5}^{2}+{6}^{2}-4×(\frac{9}{2})^{2}}$=$\frac{3.5}{5}=0.7$,
$\widehat{a}$=$\overline{y}-\widehat{b}\overline{x}$=3.5-0.7×4.5=0.35,
过(4,3)和(5,4)的直线方程为:$\frac{y-3}{4-3}=\frac{x-4}{5-4}$,
即y=x-1,则b=1,a=-1,
则$\widehat{b}$<b,$\widehat{a}$>a,
故选:C.
点评 本题考查线性回归方程的求解,以及由两点求直线方程的应用,比较基础.

练习册系列答案
相关题目
18.$\frac{1+cos20°}{2sin20°}$-sin10°(tan-15°-tan5°)=( )
| A. | $\sqrt{3}$ | B. | 1 | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
5.在△ABC中,角A、B的对边分别为a、b且A=2B,sinB=$\frac{4}{5}$,则$\frac{a}{b}$的值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{5}$ |
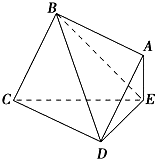 正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.
正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.