题目内容
15.若(1+x)n的展开式中x2项的系数为an,则$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$的值( )| A. | 一定大于2 | B. | 一定小于2 | C. | 等于2 | D. | 一定大于$\frac{3}{2}$ |
分析 由题意首先利用二项展开式求出an,然后求数列的和.
解答 解:因为(1+x)n的展开式中x2项的系数为an=${C}_{n}^{2}$=$\frac{n(n-1)}{2}$,
所以$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$=2[$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{(n-1)n}$]=2(1-$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n-1}-\frac{1}{n})$=2(1-$\frac{1}{n}$);
所以$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$的值一定小于2;
故选B
点评 本题考查了二项展开式的项的系数以及拆项法求数列的和;关键是正确求出an,然后根据通项特点求和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.在△ABC中,角A、B的对边分别为a、b且A=2B,sinB=$\frac{4}{5}$,则$\frac{a}{b}$的值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{5}$ |
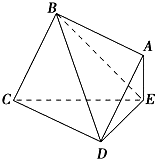 正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.
正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.