题目内容
(本题满分5分)已知函数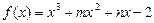 的图象过点(—1,—6),且函数
的图象过点(—1,—6),且函数 的图象关于y轴对称。 (1)求m、n的值及函数y=f(x)的单调区间;(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
的图象关于y轴对称。 (1)求m、n的值及函数y=f(x)的单调区间;(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值. 

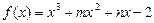 的图象过点(—1,—6),且函数
的图象过点(—1,—6),且函数 的图象关于y轴对称。 (1)求m、n的值及函数y=f(x)的单调区间;(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
的图象关于y轴对称。 (1)求m、n的值及函数y=f(x)的单调区间;(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值. 

(Ⅰ)m=-3, n=0单调递减区间是(0,2) (Ⅱ) :当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,f(x)有极小值-6,极大值;当a=1或a≥3时,f(x)无极值
(I)由函数f(x)图象过点(-1,-6),得m-n="-3," …………①…………1分
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n;
而g(x)图象关于y轴对称,所以- =0,所以m=-3,………………3分
=0,所以m=-3,………………3分
代入①得n=0……………………5分
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);……………………6分
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2)……………………6分
(II)由(Ⅰ)得f′(x)=3x(x-2), 令f′(x)=0得x=0或x=2.
当x变化时,f′(x)、f(x)的变化情况如下表:
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;…………9分
当a=1时,f(x)在(a-1,a+1)内无极值;………………11分
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;…………13分
当a≥3时,f(x)在(a-1,a+1)内无极值………………15分
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,f(x)有极小值-6,
无极大值;当a=1或a≥3时,f(x)无极值
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n;
而g(x)图象关于y轴对称,所以-
 =0,所以m=-3,………………3分
=0,所以m=-3,………………3分代入①得n=0……………………5分
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);……………………6分
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2)……………………6分
(II)由(Ⅰ)得f′(x)=3x(x-2), 令f′(x)=0得x=0或x=2.
当x变化时,f′(x)、f(x)的变化情况如下表:
| X | (-∞.0) | 0 | (0,2) | 2 | (2,+ ∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;…………9分
当a=1时,f(x)在(a-1,a+1)内无极值;………………11分
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;…………13分
当a≥3时,f(x)在(a-1,a+1)内无极值………………15分
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,f(x)有极小值-6,
无极大值;当a=1或a≥3时,f(x)无极值

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
 在两个极值点
在两个极值点 ,且
,且 。
。 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 的区域;
的区域;

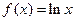 ,
,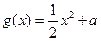 (
(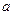 为常数),若直线
为常数),若直线 与
与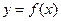 和
和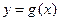 的图象都相切,且
的图象都相切,且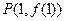 . (1)求直线
. (1)求直线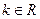 时,讨论关于
时,讨论关于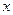 的方程
的方程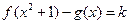 的实数解的个数.
的实数解的个数.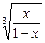 .
.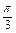 ;
;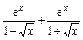 ,x0=2;
,x0=2;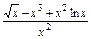 ,x0=1.
,x0=1.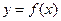 是定义域为R的偶函数,其图像均在x轴的上方,对任意的
是定义域为R的偶函数,其图像均在x轴的上方,对任意的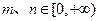 ,都有
,都有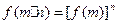 ,且
,且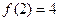 ,又当
,又当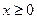 时,其导函数
时,其导函数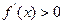 恒成立。
恒成立。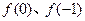 的值;
的值;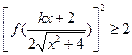 ,其中
,其中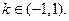
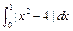 =" " ( )
=" " ( )







 ,
, =
= ,
, ,则
,则 是( )
是( )


