题目内容
设函数 ,其中
,其中 为常数.
为常数.
(1)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(2)若函数 的有极值点,求
的有极值点,求 的取值范围及
的取值范围及 的极值点;
的极值点;
(3)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.
 ,其中
,其中 为常数.
为常数.(1)当
 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;(2)若函数
 的有极值点,求
的有极值点,求 的取值范围及
的取值范围及 的极值点;
的极值点;(3)求证对任意不小于3的正整数
 ,不等式
,不等式 都成立.
都成立.(1)函数 在定义域
在定义域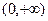 上单调递增.
上单调递增.
(2)当且仅当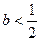 时
时 有极值点;当
有极值点;当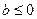 时,
时, 有唯一最小值点
有唯一最小值点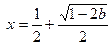 ;当
;当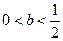 时,
时, 有一个极大值点
有一个极大值点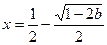 和一个极小值点
和一个极小值点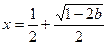
(3)证明见解析。
 在定义域
在定义域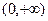 上单调递增.
上单调递增.(2)当且仅当
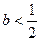 时
时 有极值点;当
有极值点;当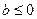 时,
时, 有唯一最小值点
有唯一最小值点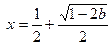 ;当
;当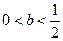 时,
时, 有一个极大值点
有一个极大值点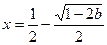 和一个极小值点
和一个极小值点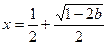
(3)证明见解析。
(1)由题意知, 的定义域为
的定义域为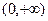 ,
,
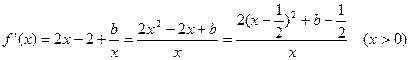 …… 1分
…… 1分
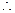 当
当 时,
时,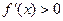 ,函数
,函数 在定义域
在定义域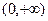 上单调递增. …… 2分
上单调递增. …… 2分
(2)①由(Ⅰ)得,当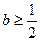 时,
时,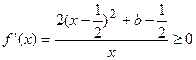 函数
函数 无极值点.
无极值点.
………3分
②当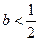 时,
时, 有两个不同解,
有两个不同解,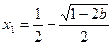
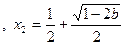
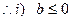 时,
时,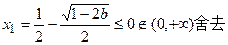 ,
,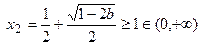
此时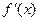 ,
, 随
随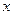 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
由此表可知: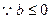 时,
时, 有唯一极小值点
有唯一极小值点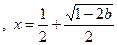 , …… 5分
, …… 5分
ii) 当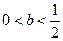 时,0<
时,0< <1 此时,
<1 此时,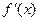 ,
, 随
随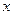 的变化情况如下表:
的变化情况如下表:
由此表可知: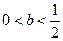 时,
时, 有一个极大值
有一个极大值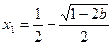 和一个极小值点
和一个极小值点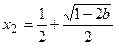 ;综上所述:当且仅当
;综上所述:当且仅当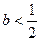 时
时 有极值点;当
有极值点;当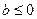 时,
时, 有唯一最小值点
有唯一最小值点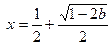 ;当
;当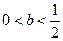 时,
时, 有一个极大值点
有一个极大值点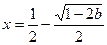 和一个极小值点
和一个极小值点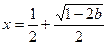 …… 8分
…… 8分
(3)由(2)可知当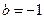 时,函数
时,函数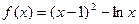 ,
,
此时 有唯一极小值点
有唯一极小值点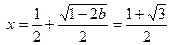
且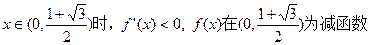 …… 9分
…… 9分
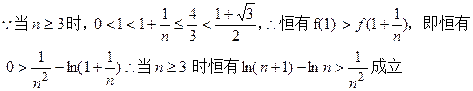
…… 11分
令函数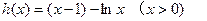
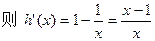 …… 12分
…… 12分
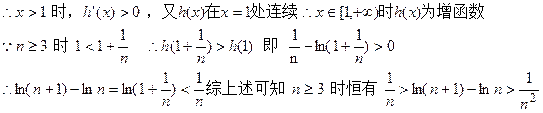 …… 14分
…… 14分
 的定义域为
的定义域为 ,
,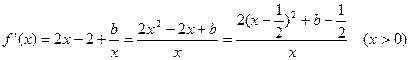 …… 1分
…… 1分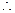 当
当 时,
时,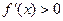 ,函数
,函数 在定义域
在定义域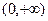 上单调递增. …… 2分
上单调递增. …… 2分(2)①由(Ⅰ)得,当
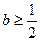 时,
时,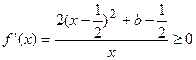 函数
函数 无极值点.
无极值点.………3分
②当
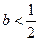 时,
时, 有两个不同解,
有两个不同解,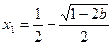
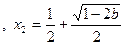
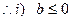 时,
时,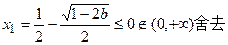 ,
,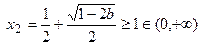
此时
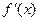 ,
, 随
随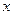 在定义域上的变化情况如下表:
在定义域上的变化情况如下表: |  | 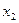 | 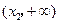 |
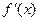 | 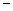 | 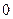 | 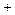 |
 | 减 | 极小值 | 增 |
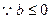 时,
时, 有唯一极小值点
有唯一极小值点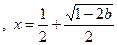 , …… 5分
, …… 5分ii) 当
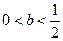 时,0<
时,0< <1 此时,
<1 此时,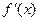 ,
, 随
随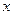 的变化情况如下表:
的变化情况如下表: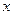 | 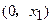 | 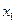 | 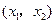 | 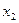 | 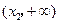 |
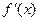 | 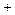 |  |  |  |  |
 | 增 | 极大值 | 减 | 极小值 | 增 |
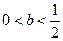 时,
时, 有一个极大值
有一个极大值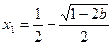 和一个极小值点
和一个极小值点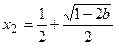 ;综上所述:当且仅当
;综上所述:当且仅当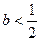 时
时 有极值点;当
有极值点;当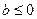 时,
时, 有唯一最小值点
有唯一最小值点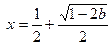 ;当
;当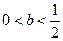 时,
时, 有一个极大值点
有一个极大值点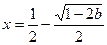 和一个极小值点
和一个极小值点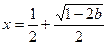 …… 8分
…… 8分(3)由(2)可知当
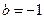 时,函数
时,函数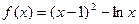 ,
,此时
 有唯一极小值点
有唯一极小值点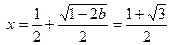
且
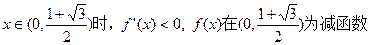 …… 9分
…… 9分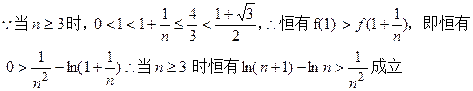
…… 11分
令函数
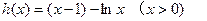
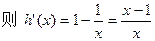 …… 12分
…… 12分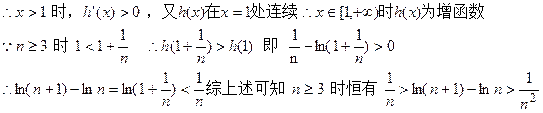 …… 14分
…… 14分
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 数
数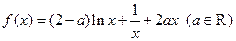
 (1)当
(1)当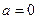 时,求
时,求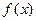 的极值;(2)当
的极值;(2)当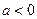 时,求
时,求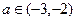 及
及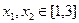 ,恒有
,恒有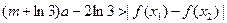 成立,求
成立,求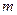 的取值范围
的取值范围
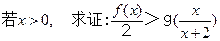
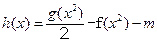 恰有四个不同的零点?若存在求出的m范围;若不存在,说明理由。
恰有四个不同的零点?若存在求出的m范围;若不存在,说明理由。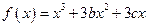 在两个极值点
在两个极值点 ,且
,且 。
。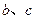 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 的区域;
的区域;

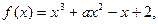
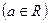
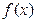 在
在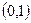 上是减函数,求
上是减函数,求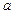 的最大值;
的最大值;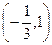 ,求函数y=
,求函数y=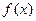 图像过点
图像过点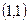 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。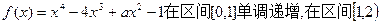 单调递减,
单调递减,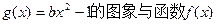 的图象恰有3个交点,若
的图象恰有3个交点,若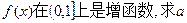 的取值范围数b的值;若不存在,试说明理由。
的取值范围数b的值;若不存在,试说明理由。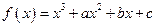 ,在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,当且仅当x>4时,
,在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,当且仅当x>4时,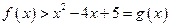 .
.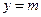 与函数f(x)、g(x)的图象共有3个交点,求m的取值范围.
与函数f(x)、g(x)的图象共有3个交点,求m的取值范围.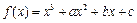 在
在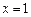 和
和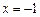 时取极值,且
时取极值,且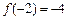 .
.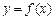 的表达式;
的表达式;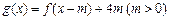 在区间
在区间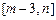 上的值域为
上的值域为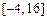 ,试求
,试求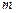 、n应满足的条件。
、n应满足的条件。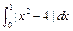 =" " ( )
=" " ( )


