题目内容
在乒乓球比赛中,甲与乙以“五局三胜”制进行比赛,根据以往比赛情况,甲在每一局胜乙的概率均为  .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求:
(Ⅰ)甲在这种情况下取胜的概率;
(Ⅱ)设比赛局数为X,求X的分布列及数学期望(均用分数作答)。
(Ⅰ) 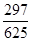 (Ⅱ)见解析
(Ⅱ)见解析
解析试题分析:(Ⅰ) 由题知,在乙先赢了第一局的情况下,甲取胜是两个互斥事件的和,其概率用互斥事件的和概率公式计算,其中一个事件,比赛四局,第一局乙赢的条件下,后三局甲赢,因甲每局胜的概率相同,其概率按独立重复试验计算,另一事件为,比赛五局,在第一局乙胜的条件下,中间三局甲胜二局,其概率按独立重复试验计算,与最后一局甲胜是相互独立事件,用相互独立事件的积概率公式计算;(Ⅱ)由题意知找出X的所有可能取值,分析X取每个值时的情况,将其分解成若干个互斥简单事件的和,利用和概率公式计算,分析每个简单事件分成若干个相互独立事件的积,利用积概率公式计算其概率,列出分布列,求出期望.
试题解析:(Ⅰ)甲取胜的概率为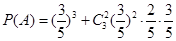 =
=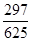 (4分)
(4分)
(Ⅱ)由题意知X=3,4,5,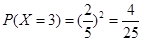
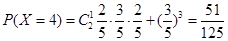
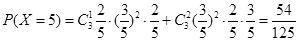
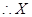 的分布列为:
的分布列为:
3 4 5 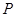

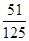
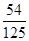
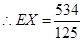 .12分
.12分
考点:独立重复试验,互斥事件的和概率公式,相互独立事件的积概率公式,离散型随机变量分布列及其期望,应用意识

练习册系列答案
相关题目
 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有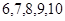 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有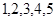 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜. ;
; 为取出2球中白球的个数,已知
为取出2球中白球的个数,已知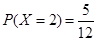 .
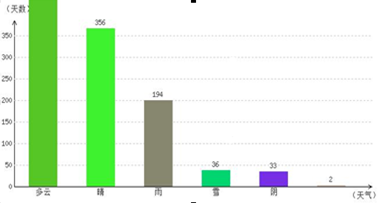
.
 的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为2元或40元;在非雨雪天的情况下,他以90%的概率骑自行车上班,每天交通费用0元;另外以10%的概率打出租上班,每天交通费用20元。(以频率代替概率,保留两位小数.参考数据:
的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为2元或40元;在非雨雪天的情况下,他以90%的概率骑自行车上班,每天交通费用0元;另外以10%的概率打出租上班,每天交通费用20元。(以频率代替概率,保留两位小数.参考数据: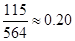 )
) 、
、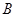 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 个红球与
个红球与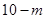 个白球,盒子
个白球,盒子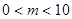 ).
). 表示红球的个数;
表示红球的个数;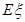 等于定值;
等于定值;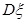 取到最小值,并求出最小值.
取到最小值,并求出最小值.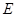 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率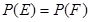 ,求
,求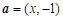 ,
, ,其中
,其中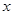 随机选自集合
随机选自集合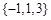 ,
,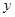 随机选自集合
随机选自集合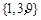 ,那么
,那么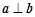 的概率是 .
的概率是 .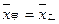 ,方差
,方差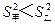 ,则成绩较稳定的同学是 (填“甲”或“乙”)
,则成绩较稳定的同学是 (填“甲”或“乙”)