题目内容
下图是淮北市6月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择6月1日至6月15日中的某一天到达该市,并停留2天.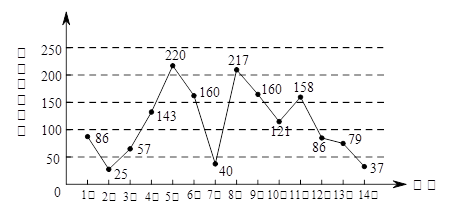
(1)求此人到达当日空气重度污染的概率;
(2)若设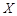 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
(3)由图判断从哪天开始淮北市连续三天的空气质量指数方差最大?(结论不要求证明)
(1) (2)
(2) (3)6月5日
(3)6月5日
解析试题分析:(1)考察认识图的能力,通过图计算出优良、重度污染的天数,这是做古典概型题的关键.(2)根据概率计算公式去事件发生的概率.(3)判断是否为古典概型,看这个实验是否具有有限性和等可能性两个特点,尤其等可能性,这是容易漏掉的地方.(4)有时考虑使用对立事件的概率公式.
试题解析:解:设 表示事件“此人于6月
表示事件“此人于6月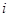 日到达该市”(
日到达该市”( 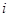 =1,2,…,13).
=1,2,…,13).
根据题意, 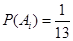 ,且
,且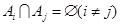 .
.
(1)设B为事件“此人到达当日空气重度污染”,则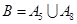 ,
,
所以 . 3分
. 3分
(2)由题意可知,X的所有可能取值为0,1,2,
P(X=0)=1-P(X=1)-P(X="2)=" 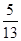 ,
,
P(X=1)=P(A3∪A6∪A7∪A11)= P(A3)+P(A6)+P(A7)+P(A11)=  ,
,
P(X=2)=P(A1∪A2∪A12∪A13)= P(A1)+P(A2)+P(A12)+P(A13)=  , 9分
, 9分
(3)从6月5日开始连续三天的空气质量指数方差最大. 12分
考点:随机事件发生的概率.

练习册系列答案
相关题目
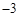 为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是____.
为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是____. 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有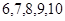 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有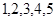 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.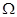 ;
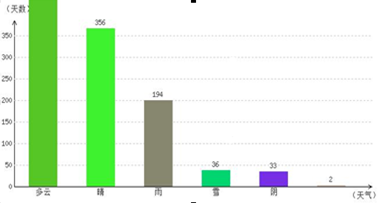
;
 的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为2元或40元;在非雨雪天的情况下,他以90%的概率骑自行车上班,每天交通费用0元;另外以10%的概率打出租上班,每天交通费用20元。(以频率代替概率,保留两位小数.参考数据:
的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为2元或40元;在非雨雪天的情况下,他以90%的概率骑自行车上班,每天交通费用0元;另外以10%的概率打出租上班,每天交通费用20元。(以频率代替概率,保留两位小数.参考数据: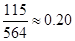 )
) (单位:元),求
(单位:元),求