题目内容
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有
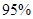 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望.
附:
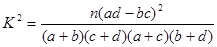 ,其中
,其中 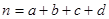
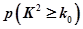 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(1)关注NBA与性别有关;(2)分布列(略),E(X)=1.
解析试题分析:(1)本小题独立性检测的应用,本小题的关键是计算出 为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表: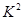 的观测值
的观测值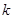 ,和
,和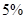 对应的临界值
对应的临界值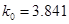 ,根据关注NBA的学生的概率为
,根据关注NBA的学生的概率为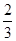 ,可知关注NBA的学生为32(估计值).根据条件填满表格,然后计算出
,可知关注NBA的学生为32(估计值).根据条件填满表格,然后计算出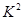 ,并判断其与
,并判断其与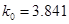 的大小关系,得出结论.(2)对于分布列问题:首先应弄清随机变量是谁以及随机变量的取值范围,然后就是每个随机变量下概率的取值,最后列表计算期望.
的大小关系,得出结论.(2)对于分布列问题:首先应弄清随机变量是谁以及随机变量的取值范围,然后就是每个随机变量下概率的取值,最后列表计算期望.
试题解析:
(1)将列联表补充完整有:
由 关注NBA 不关注NBA 合 计 男生 22 6 28 女生 10 10 20 合计 32 16 48 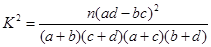 ,计算可得
,计算可得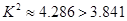 4分
4分
因此,在犯错的概率不超过0.05的前提下认为学生关注NBA与性别有关,
即有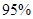 把握认为关注NBA与性别有关 6分
把握认为关注NBA与性别有关 6分
(2)由题意可知,X的取值为0,1,2,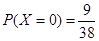 ,
,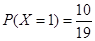 ,
,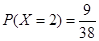 9分
9分
所以X的分布列为X 0 1 2 p 
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
喜爱打篮球
不喜爱打篮球
合计
男生
5
女生
10
合计
50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .(12分)
.(12分)
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为 ,求
,求 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
0.15
0.10
0.05[
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式: ,其中
,其中 )
)
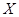 为取出2球中白球的个数,已知
为取出2球中白球的个数,已知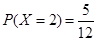 .
. (已知甲回答每道题的正确率相同,并且相互之间没有影响).
(已知甲回答每道题的正确率相同,并且相互之间没有影响). .
.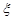 的数学期望和方差.
的数学期望和方差.
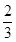 ,则
,则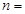 __________
__________