题目内容
14．函数y=2x2-x-1的值域是[-$\frac{9}{8}$，+∞）．分析 利用配方法化简可得y=2x2-x-1=2（x-$\frac{1}{4}$）2-$\frac{9}{8}$，从而求函数的值域．
解答 解：y=2x2-x-1=2（x-$\frac{1}{4}$）2-$\frac{9}{8}$≥-$\frac{9}{8}$，
故函数y=2x2-x-1的值域是[-$\frac{9}{8}$，+∞）；
故答案为：[-$\frac{9}{8}$，+∞）．
点评 本题考查了函数的值域的求法，属于基础题．
练习册系列答案
相关题目
19．
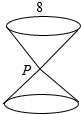如图，某计时沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8，用一个平行于圆锥沙漏的轴的平面α截圆锥，得到的截口曲线为双曲线的一部分，且圆锥顶点P到平面α的距离为2，则此双曲线的离心率为（ ）
如图，某计时沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8，用一个平行于圆锥沙漏的轴的平面α截圆锥，得到的截口曲线为双曲线的一部分，且圆锥顶点P到平面α的距离为2，则此双曲线的离心率为（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |