题目内容
5.实数x,y满足x-3$\sqrt{x+1}$=3$\sqrt{y+2}$-y,则x+y的最小值为$\frac{9+3\sqrt{21}}{2}$,最大值为9+3$\sqrt{15}$.分析 令a=$\sqrt{x+1}$(a≥0),b=$\sqrt{y+2}$(b≥0),则x=a2-1,y=b2-2,即为(a-$\frac{3}{2}$)2+(b-$\frac{3}{2}$)2=$\frac{15}{2}$,其几何意义为以C($\frac{3}{2}$,$\frac{3}{2}$)为圆心,$\frac{\sqrt{30}}{2}$为半径的圆弧(位于第一象限),则x+y=a2+b2-3,其几何意义是点(a,b)与原点的距离的平方与3的差.画出圆弧,运用圆的性质,即可计算得到最值.
解答 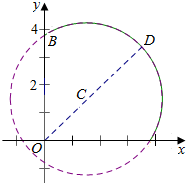 解:令a=$\sqrt{x+1}$(a≥0),b=$\sqrt{y+2}$(b≥0),
解:令a=$\sqrt{x+1}$(a≥0),b=$\sqrt{y+2}$(b≥0),
则x=a2-1,y=b2-2,
即有a2-1-3a=3b-(b2-2),
即为(a-$\frac{3}{2}$)2+(b-$\frac{3}{2}$)2=$\frac{15}{2}$,
其几何意义为以C($\frac{3}{2}$,$\frac{3}{2}$)为圆心,
$\frac{\sqrt{30}}{2}$为半径的圆弧(位于第一象限),
则x+y=a2+b2-3,其几何意义是点(a,b)与原点的距离的平方与3的差.
由右图可得OA(或OB)最短,连接OC延长交圆于D,则OD最长.
则|OD|=|OC|+|CD|=$\frac{3\sqrt{2}}{2}$+$\frac{\sqrt{30}}{2}$=$\frac{3\sqrt{2}+\sqrt{30}}{2}$;
由(a-$\frac{3}{2}$)2+(b-$\frac{3}{2}$)2=$\frac{15}{2}$,令a=0(或b=0)则b=$\frac{3+\sqrt{21}}{2}$(或a=$\frac{3+\sqrt{21}}{2}$),
|OA|=|OB|=$\frac{3+\sqrt{21}}{2}$,
则x+y的最大值为9+3$\sqrt{15}$,最小值为$\frac{9+3\sqrt{21}}{2}$.
故答案为:9+3$\sqrt{15}$,$\frac{9+3\sqrt{21}}{2}$.
点评 本题考查给出条件求最值,主要考查换元法和圆的方程的运用,考查数形结合和运算能力,属于中档题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | R | B. | (-∞,1)∪(1,+∞) | C. | (-∞,2)∪(2,+∞) | D. | (-∞,1)∪(2,+∞) |