题目内容
9.对于m的不同的取值范围,讨论方程x2-4|x|+5=m的实数根个数.分析 根据题意作出y=x2-4|x|+5的图象,分析直线y=m与y=x2-4|x|+5的图象交点个数,从而可得结论.
解答 解:设f(x)=x2-4|x|+5,
则f(x)=$\left\{\begin{array}{l}{x}^{2}-4x+5,x≥0\\{x}^{2}+4x+5,x<0\end{array}\right.$,
作出f(x)的图象,如图所示: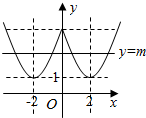
当m<1时,函数f(x)与y=m的图象无交点,方程x2-4|x|+5=m有0个实根;
当m=1,或x>5时,函数f(x)与y=m的图象有两个交点,方程x2-4|x|+5=m有2个实根;
当m=5时,函数f(x)与y=m的图象有三个交点,方程x2-4|x|+5=m有3个实根;
当1<x<5时,函数f(x)与y=m的图象有四个交点,方程x2-4|x|+5=m有4个实根;
点评 考查学生会根据解析式作出相应的函数图象,会根据直线与函数图象交点的个数得到方程解的个数.注意利用数形结合的数学思想解决实际问题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目