题目内容
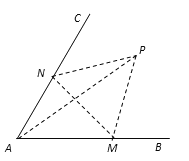
【题目】如图，经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N （异于村庄A),要求PM＝PN＝MN＝2（单位:千米)．如何设计, 可以使得工厂产生的噪声对居民的影响最小（即工厂与村庄的距离最远)．
【答案】当
为
时，工厂产生的噪声对居民的影响最小。
【解析】
试题分析：根据题意，设
，则
，在
中，根据正弦定理得：
，整理得：
，那么在
中，由余弦定理得：
，又因为
，所以代入上式得：，从而得到关于变量
的函数关系式，最后通过化简整理得到关于的正弦型函数，再求
的最大值，从而求出
的最大值。本题考查解三角形的实际应用，主要是研究图形，利用题中的已知条件，将正弦、余弦定理应用在解题中。考查学生对知识的综合运用能力。
试题解析：设，在中，．
因为
，所以．
在中，
．
当且仅当
，即
时，
取得最大值12，即
取得最大值
．
答：设为时，工厂产生的噪声对居民的影响最小．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
