题目内容
18.已知a,b,c为三角形的三边且S=a2+b2+c2,P=ab+bc+ca,则 ( )| A. | S≥2P | B. | P<S<2P | C. | S>P | D. | P≤S<2P |
分析 由于a+b>c,a+c>b,c+b>a,可得ac+bc>c2,ab+bc>b2,ac+ab>a2,可得SP>S.又2S-2P=(a-b)2+(a-c)2+(b-c)2≥0,可得S≥P,即可得出.
解答 解:∵a+b>c,a+c>b,c+b>a,
∴ac+bc>c2,ab+bc>b2,ac+ab>a2,
∴2(ac+bc+ab)>c2+b2+a2,
∴SP>S.
又2S-2P=(a-b)2+(a-c)2+(b-c)2≥0,
∴S≥P>0.
∴P≤S<2P.
故选:D.
点评 本题考查了基本不等式的性质、三角形三边大小关系,考查了变形能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.5名高中毕业生报考三所重点院校,每人限报且只报一所院校,则不同的报名方法有( )
| A. | 35种 | B. | 53种 | C. | 60种 | D. | 10种 |
7.已知数列{an}的通项公式an=$\frac{n+1}{n+2}$(n∈N+),设{an}的前n项积为sn,则使sn<$\frac{1}{32}$成立的自然数n( )
| A. | 有最大值62 | B. | 有最小值63 | C. | 有最大值62 | D. | 有最小值31 |
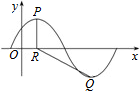 已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$
已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$