题目内容

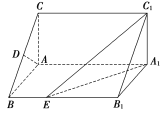
【题目】在空间四边形ABCD中，AB＝CD，AB与CD成30°角，E，F分别为BC，AD的中点，求EF与AB所成的角．

【答案】或

【解析】试题分析：取的中点，连接，因为分别为的中点，根据三角形中位线定理可得， 就是与所成的角， 与所成角为，所以或，利用等腰三角形的性质可得结果.

试题解析：取BD的中点G，连接EG，FG，因为E，F分别为BC，AD的中点，所以且， 且

所以EG与GF所成的角即为AB与CD所成的角，因为AB＝CD，所以△EFG为等腰三角形．

又AB与CD所成角为30°，所以∠EGF＝30°或150°，因为∠GFE就是EF与AB所成的角，所以EF与AB所成角为75°或15°.

【方法点晴】本题主要考查异面直线所成的角，属于中档题题.求异面直线所成的角的角先要利用三角形中位线定理以及平行四边形找到，异面直线所成的角，然后利用直角三角形的性质及余弦定理求解，如果利用余弦定理求异面直线所成角的余弦，因为异面直线所成的角是直角或锐角，所以最后结果一定要取绝对值.

练习册系列答案
相关题目

【题目】函数， ．

（Ⅰ）讨论的极值点的个数；

（Ⅱ）若对于任意，总有成立，求实数的取值范围.

【题目】【2016高考江苏卷】已知函数.设.

（1）求方程的根;

（2）若对任意,不等式恒成立，求实数的最大值；

（3）若，函数有且只有1个零点，求的值。

【题目】若有穷数列（是正整数），满足即（是正整数，且），就称该数列为“对称数列”。例如，数列与数列都是“对称数列”．

（1）已知数列是项数为9的对称数列，且,,,,成等差数列， ， ,试求， ， ， ，并求前9项和.

（2）若是项数为的对称数列，且构成首项为31，公差为的等差数列，数列前项和为，则当为何值时， 取到最大值？最大值为多少？

（3）设是项的“对称数列”，其中是首项为1，公比为2的等比数列．求前项的和 ．

【题目】以直角坐标系的原点为极点， 轴的正半轴为极轴，并在两种坐标系中取相同的长度单位，点的极坐标为，圆以为圆心，4为半径；又直线的极坐标方程为。

（Ⅰ）求直线和圆的普通方程；

（Ⅱ）试判定直线和圆的位置关系．若相交，则求直线被圆截得的弦长．

【题目】已知函数f(x)＝(λx＋1)ln x－x＋1.

(1)若λ＝0，求f(x)的最大值；

(2)若曲线y＝f(x)在点(1，f(1))处的切线与直线x＋y＋1＝0垂直，证明：>0.

【题目】已知在的展开式中，第5项的系数与第3项的系数之比是56：3．

（1）求展开式中的所有有理项；

（2）求展开式中系数绝对值最大的项．

（3）求的值.

【题目】【2017长沙模拟】如图，在直棱柱ABCA1B1C1中，∠BAC＝90°，AB＝AC＝，AA1＝3，D是BC的中点，点E在棱BB1上运动．

(1)求证：AD⊥C1E；

(2)当异面直线AC，C1E所成的角为60°时，求三棱锥C1A1B1E的体积．

【题目】某医学院读书协会欲研究昼夜温差大小与患感冒人数多少之间的关系，该协会分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下频数分布直方图：

该协会确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验.

（1）求选取的2组数据恰好是相邻两个月的频率；

（2）已知选取的是1月与6月的两组数据.

（i）请根据2至5月份的数据，求出就诊人数关于昼夜温差的线性回归方程；

（ii）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该协会所得线性回归方程是否理想？

（参考公式：，）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网