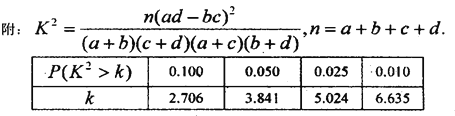题目内容
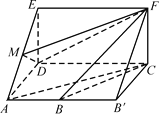
【题目】已知长方形ABCD中,AB=3,AD=4.现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
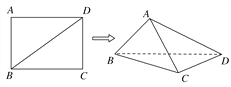
(1)试问:在折叠的过程中,直线AB与CD能否垂直?若能,求出相应a的值;若不能,请说明理由;
(2)求四面体A-BCD体积的最大值.
【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)假设![]() ,又
,又![]() ,则
,则![]() 平面
平面![]() ,得到
,得到![]() ,解得
,解得![]() ;(2)易知,翻折到平面
;(2)易知,翻折到平面![]() 平面
平面![]() 时,体积最大,则底面为
时,体积最大,则底面为![]() ,高为
,高为![]() ,求得最大体积为
,求得最大体积为![]() 。
。
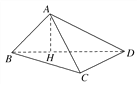
(1)直线AB与CD能够垂直.
因为AB⊥AD,若AB⊥CD,AD∩CD=D,
则有AB⊥平面ACD,
从而AB⊥AC.
此时,a=![]() =
=![]() =
=![]() ,
,
即当a=![]() 时,有AB⊥CD.
时,有AB⊥CD.
(2)由于△BCD面积为定值,所以当点A到平面BCD的距离最大,即当平面ABD⊥平面BCD时,该四面体的体积最大,
此时,过点A在平面ABD内作AH⊥BD,垂足为H,
则有AH⊥平面BCD,AH就是该四面体的高.
在△ABD中,AH=![]() =
=![]() ,
,
S△BCD=![]() ×3×4=6,
×3×4=6,
此时VA-BCD=![]() S△BCD·AH=
S△BCD·AH=![]() ,即为该四面体体积的最大值.
,即为该四面体体积的最大值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运
会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.