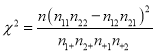题目内容
【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列![]() 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-![]() 的大小.
的大小.
【答案】见解析
【解析】(1)设数列{an}的公差为d.
因为a1=1,且a1,a2,a5依次成等比数列,
所以a=a1·a5,即(1+d)2=1·(1+4d),
所以d2-2d=0,解得d=2(d=0不合要求,舍去).
所以an=1+2(n-1)=2n-1.
因为bn+1=2bn-1,所以bn+1-1=2(bn-1).
所以{bn-1}是首项为b1-1=2,公比为2的等比数列.
所以bn-1=2×2n-1=2n.
所以bn=2n+1.
(2)因为![]() =
=![]() =
=![]() -
-![]() ,
,
所以Sn=![]() +
+![]() +…+
+…+![]() =1-
=1-![]() ,
,
于是Sn-![]() =1-
=1-![]() -1+
-1+![]() =
=![]() -
-![]() =
=![]() .
.
所以当n=1,2时,2n=2n,Sn=1-![]() ;
;
当n≥3时,2n<2n,Sn<1-![]() .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本,对高一年级的100名学生的成绩进行统计,并按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,得到成绩分布的频率分布直方图(如图)。
分组,得到成绩分布的频率分布直方图(如图)。

(1)若规定60分以上(包括60分)为合格,计算高一年级这次竞赛的合格率;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
(3)若高二年级这次竞赛的合格率为![]() ,由以上统计数据填写下面
,由以上统计数据填写下面![]() 列联表,并问是否有
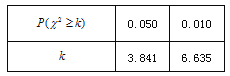
列联表,并问是否有![]() 的把握认为“这次知识竞赛的成绩与年级有关”。
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
 附:参考数据与公式
附:参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |