题目内容
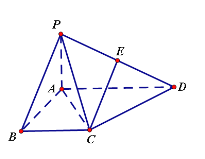
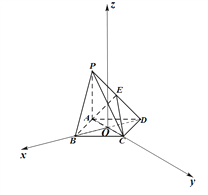
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 为
为![]() 上一点.
上一点.
(1)若![]() 平面
平面![]() ,试说明点
,试说明点![]() 的位置并证明的结论;
的位置并证明的结论;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,且
,且![]() ,
,
求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)当点![]() 为
为![]() 中点时有
中点时有![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,由
,由![]() 为菱形得
为菱形得![]() 是
是![]() 的中点,由三角形的中位线性质可得
的中点,由三角形的中位线性质可得![]() ,即可证明
,即可证明![]() ;(2)以
;(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴和
轴和![]() 轴建立空间直角坐标系,分别求得平面
轴建立空间直角坐标系,分别求得平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,结合图形得二面角
的法向量,结合图形得二面角![]() 为锐二面角,即可求得二面角
为锐二面角,即可求得二面角![]() 的余弦值.
的余弦值.
试题解析:(1)当点![]() 为
为![]() 中点时有
中点时有![]() ,证明如下:
,证明如下:
连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
由菱形性质知点![]() 是
是![]() 的中点.
的中点.
∴![]()
又∵![]()
∴![]() .
.
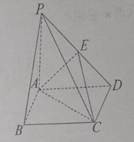
(2)由题意,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴和
轴和![]() 轴建立如图所示的空间直角坐标系,设
轴建立如图所示的空间直角坐标系,设![]() ,则由条件易知
,则由条件易知![]() ,所以,
,所以,![]() .
.
∴![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() .
.
∴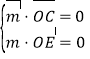 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,所以,
,所以,![]()
同理可求平面![]() 的法向量
的法向量![]() .
.
所以,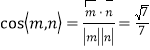 .
.
由图可知,二面角![]() 为锐二面角,故其余弦值为
为锐二面角,故其余弦值为![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 4 | 6 | 7 | 8 | 10 |
销量 | 60 | 50 | 45 | 30 | 20 |
(1) 请根据上表提供的数据画出散点图,并判断是正相关还是负相关;
(2) 求出![]() 关于
关于![]() 的回归直线方程,若单价为9元时,预测其销量为多少?
的回归直线方程,若单价为9元时,预测其销量为多少?
(参考公式:回归直线方程中公式 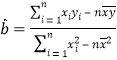 ,
,![]() )
)
【题目】下表数据为某地区某种农产品的年产量x(单位:吨)及对应销售价格y(单位:千元/吨) .
x | 1 | 2 | 3 | 4 | 5 |
y | 70 | 65 | 55 | 38 | 22 |
(1)若y与x有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程.
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润Z最大?
(参考公式:回归直线方程为![]() ,
,![]() ,
,![]() )
)