题目内容
3.已知a>0,函数f(x)=-2asin(2x+$\frac{π}{6}$)+2a+b,x∈[0,$\frac{π}{2}}$]时,f(x)的值域为[-5,1].(1)求常数a,b的值;
(2)设 g(x)=f(x+$\frac{π}{2}$)且g(x)的定义域为不等式lg[g(x)]>0的解集,求g(x)的单调区间.
分析 (1)由条件利用正弦函数的定义域和值域,求得f(x)∈[b,3a+b],又已知-5≤f(x)≤1,从而求得常数a,b的值.
(2)由条件可得4sin(2x+$\frac{π}{6}$)-1>1,即sin(2x+$\frac{π}{6}$)>$\frac{1}{2}$,∴2kπ+$\frac{π}{6}$<2x+$\frac{π}{6}$<2kπ+$\frac{5π}{6}$,k∈Z.再结合正弦函数的单调性求得它的单调区间.
解答 解:(1)∵x∈[0,$\frac{π}{2}}$],∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$].
∴sin (2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],∴-2asin(2x+$\frac{π}{6}$)∈[-2a,a].
∴f(x)∈[b,3a+b],又∵-5≤f(x)≤1,
∴b=-5,3a+b=1,因此a=2,b=-5.
(2)由(1)得,f(x)=-4sin (2x+$\frac{π}{6}$)-1,
g(x)=f (x+$\frac{π}{2}$)=-4sin(2x+$\frac{7π}{6}$)-1=4sin(2x+$\frac{π}{6}$)-1.
又由lg g(x)>0,得g(x)>1,∴4sin(2x+$\frac{π}{6}$)-1>1,
∴sin(2x+$\frac{π}{6}$)>$\frac{1}{2}$,∴2kπ+$\frac{π}{6}$<2x+$\frac{π}{6}$<2kπ+$\frac{5π}{6}$,k∈Z.
其中当2kπ+$\frac{π}{6}$<2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z时,g(x)单调递增,即kπ<x≤kπ+$\frac{π}{6}$,k∈Z,
∴g(x)的单调增区间为(kπ,kπ+$\frac{π}{6}$],k∈Z.
又∵当2kπ+$\frac{π}{2}$<2x+$\frac{π}{6}$<2kπ+$\frac{5π}{6}$,k∈Z时,g(x)单调递减,即kπ+$\frac{π}{6}$<x<kπ+$\frac{π}{3}$,k∈Z.
∴g(x)的单调减区间为 (kπ+$\frac{π}{6}$,kπ+$\frac{π}{3}$,),k∈Z.
点评 本题主要考查正弦函数的定义域和值域,解三角不等式,正弦函数的单调性,属于中档题.

| A. | 13 | B. | 53 | C. | 81 | D. | 161 |
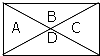 用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )| A. | 160种 | B. | 240种 | C. | 260种 | D. | 360种 |
| A. | f(x)=x3 | B. | f(x)=-|x+1| | C. | f(x)=ln$\frac{2-x}{2+x}$ | D. | f(x)=$\frac{{a}^{x}+{a}^{-x}}{2}$ |
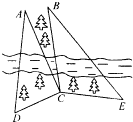 如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).
如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).