题目内容

15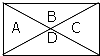．用5种不同的颜色给如图标有A，B，C，D的各部分涂色，每部分只涂一种颜色，且相邻两部分不同颜色，则不同的涂色方法共有（　　）
A．160种B．240种C．260种D．360种

分析 根据题意，先分析A区域，有5种颜色可选，即有5种涂法方案，再分①若B、D区域涂不同的颜色，②若B、D区域涂相同的颜色，两种情况讨论其他3个区域的涂色方案，由分类计数原理可得其他个区域的涂色方案的数目；再由分步计数原理计算可得答案．

解答 解：对于A区域，有5种颜色可选，即有5种涂法，
分类讨论其他3个区域：①若B、D区域涂不同的颜色，则有A42=12种涂法，C区域有3种涂法，此时其他3个区域有12×3=36种涂法；
②若B、D区域涂相同的颜色，则有4种涂法，C区域有4种涂法，此时其他3个区域有有4×4=16种涂法；
则共有5×（36+16）=5×52=260种；
故选：C．

点评 本题考查计数原理的运用，考查学生分析解决问题的能力，体现了分类讨论的数学思想，属于中档题．

练习册系列答案
相关题目
5．已知抛物线y2=$\frac{1}{4}$x，直线l与该抛物线交于A，B两点
（1）若线段AB的中点为（1，2），求直线l的方程
（2）若A，B两点到抛物线的F的距离之和为6，求直线l斜率的范围．
6．已知数列{an}的前n项和为Sn，a1=3，an+1=2an+2n+1-1（n∈N*）．
（1）求a2，a3
（2）求实数λ使{$\frac{{a}_{n}+λ}{{2}^{n}}$}为等差数列，并由此求出an与Sn；
（3）求n的所有取值，使$\frac{{S}_{n}}{{a}_{n}}$∈N*，说明你的理由．
3．已知a＞0，函数f（x）=-2asin（2x+$\frac{π}{6}$）+2a+b，x∈[0，$\frac{π}{2}}$]时，f（x）的值域为[-5，1]．
（1）求常数a，b的值；
（2）设 g（x）=f（x+$\frac{π}{2}$）且g（x）的定义域为不等式lg[g（x）]＞0的解集，求g（x）的单调区间．
10．计算$\overrightarrow{AB}$+$\overrightarrow{CA}$-$\overrightarrow{CB}$=（　　）
A．$\overrightarrow{AC}$B．$\overrightarrow{CA}$C．0D．$\overrightarrow{0}$
20．已知实数x，y满足条件$\left\{\begin{array}{l}{1≤x+y≤3}\\{-1≤x-y≤1}\end{array}\right.$，那么2x+y的取值范围是（　　）
A．[0，6]B．[2，5]C．[2，4]D．[1，5]
7．已知函数f（x）=msin2x+cos2x的图象过点（$\frac{π}{12}，\sqrt{3}$）．
（Ⅰ）求m的值；
（Ⅱ）将函数y=f（x）的图象向右平移$\frac{π}{6}$个单位得到y=g（x）的图象，求y=g（x）在区间[0，$\frac{π}{2}$]上的最大值和最小值．
4．解不等式$\frac{\sqrt{{x}^{2}+1}+{2}^{x}}{\sqrt{{x}^{2}+1}+{2}^{x+1}}$+$\frac{\sqrt{{x}^{2}+2}+{3}^{2x}}{\sqrt{{x}^{2}+2}+{3}^{2x+1}}$+$\frac{\sqrt{{x}^{2}+3}+{6}^{3x}}{\sqrt{{x}^{2}+3}+{6}^{3x+1}}$＞1．
5．集合M={x|0＜x≤3}，N={x∈N|0≤x-1≤1}，则M∩N={1，2}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网