题目内容
8.某地区预计从2015年初开始的第x月,商品A的价格f(x)=$\frac{1}{2}$(x2-12x+69)(x∈N,x≤12,价格单位:元),且第x月该商品的销售量g(x)=x+12(单位:万件).(1)商品A在2015年的最低价格是多少?
(2)2015年的哪一个月的销售收入最少,最少是多少?
分析 (1)由价格函数f(x)=$\frac{1}{2}$(x2-12x+69)(x∈N,1≤x≤12)是二次函数,可得f(x)的最小值,即价格最低;
(2)销售收入y=f(x)•g(x),整理,得关于x的三次函数,用求导法,可以求出y的最小值,即哪个月销售收入最少.
解答 解:(1)∵f(x)=$\frac{1}{2}$(x2-12x+69)=$\frac{1}{2}$[(x-6)2+33]
∴当x=6时,f(x)取得最小值,
即第6月的价格最低,最低价格为16.5元;…(4分)
(2)设第x月的销售收入为y(万元),依题意有y=$\frac{1}{2}$(x2-12x+69)(x+12)=$\frac{1}{2}$(x3-75x+828),…(6分)
∴y′=$\frac{3}{2}$(x+5)(x-5),…(8分)
∴当1≤x≤5时y′≤0,y递减;…(9分)
当5≤x≤12时y′≥0,y递增,…(10分)
∴当x=5时,y最小,即第5个月销售收入最少.最低销售收入为289万元…(12分)
答:2013年在第5月的销售收入最低.最低销售收入为289万元…(13分)
点评 本题考查了二次函数,三次函数模型的应用,利用求导法求函数的最值时,常用“导数大于0,函数单调增;导数小于0,函数单调减”来判定.

练习册系列答案
相关题目
19.若框图所给的程序运行结果为S=1,那么判断框中应填入的关于k的条件可以是( )
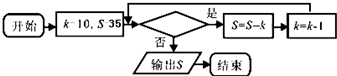

| A. | k=7 | B. | k≤6 | C. | k<6 | D. | k>6 |
20.已知实数x,y满足条件$\left\{\begin{array}{l}{1≤x+y≤3}\\{-1≤x-y≤1}\end{array}\right.$,那么2x+y的取值范围是( )
| A. | [0,6] | B. | [2,5] | C. | [2,4] | D. | [1,5] |
17.现准备将7本相同的杂志全部发给5个不同的阅读小组,其中甲、乙两个小组每个小组至少2本,其他小组允许1本也没有,则不同的分发方案共有( )
| A. | 27种 | B. | 29种 | C. | 35种 | D. | 125种 |