题目内容
11.已知集合A={x|x2+2x+p=0},B={x|x≤0},A∩B≠∅,求p的取值范围.分析 由A中方程无解,不合题意;故A中方程有解,且有解为非正数,根据B及A与B的交集不为空集,确定出p的范围即可.
解答 解:∵A={x|x2+2x+p=0},B={x|x≤0},A∩B≠∅,
∴当A=∅时,A中方程无解,不合题意;
当A≠∅时,△=4-4p≥0,即p≤1,且方程解为非正数,
A中方程解得:x=$\frac{-2±\sqrt{4-4p}}{2}$=-1±$\sqrt{1-p}$,
当x=-1-$\sqrt{1-p}$时,显然满足题意,
综上,p的范围为p≤1.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
2.在数列{an}中,a1=2,an+1=1-$\frac{1}{{a}_{n}}$,则a2010=( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
19.若框图所给的程序运行结果为S=1,那么判断框中应填入的关于k的条件可以是( )
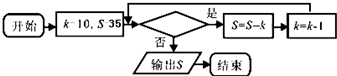

| A. | k=7 | B. | k≤6 | C. | k<6 | D. | k>6 |
20.已知实数x,y满足条件$\left\{\begin{array}{l}{1≤x+y≤3}\\{-1≤x-y≤1}\end{array}\right.$,那么2x+y的取值范围是( )
| A. | [0,6] | B. | [2,5] | C. | [2,4] | D. | [1,5] |