题目内容
已知{an}是各项均为正数的等比数列，且a1与a5的等比中项为2，则a2+a4的最小值等于______．
∵等比数列{an}，a1与a5的等比中项为2，
∴a1a5=4，
∵等比数列{an}各项均为正数，
∴a2+a4≥2
=2
=4，
当且仅当a1=a5=2时，取等号，
∴a1=a5=2时，a2+a4的最小值为4．
故答案为：4
∴a1a5=4，
∵等比数列{an}各项均为正数，
∴a2+a4≥2
| a2a4 |
| a1a5 |
当且仅当a1=a5=2时，取等号，
∴a1=a5=2时，a2+a4的最小值为4．
故答案为：4
练习册系列答案
阅读快车系列答案
相关题目
．
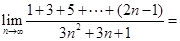