Question

11．向边长为2米的正方形木框ABCD内随机投掷一粒绿豆，记绿豆落在P点；则P点到A点的距离大于1米，同时∠DPC∈[0，$\frac{π}{2}$]的概率为1-$\frac{3π}{16}$．

Answer 1

分析 确定点P应落在两圆之外，以面积为测度，即可求出概率．

解答 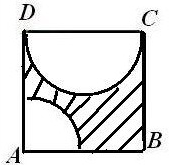解：由题意，以A点为圆心以1米为半径作圆，圆之外的所有点到A点的距离都大于1，再以DC为直径作圆，在圆上任取一点P连接P，D，C，则∠DPC为90°，圆之外的任意点与DC连线角都满足题意，由此可得点P应落在两圆之外，其面积为2×2-（$\frac{π}{4}$+$\frac{π}{2}$）=4-$\frac{3π}{4}$．
所以概率为$\frac{4-\frac{3π}{4}}{4}$=1-$\frac{3π}{16}$．
故答案为：．

点评 本题主要考查了几何概型，解题的关键是求阴影部分的面积，同时考查了计算能力，属于中档题．