题目内容
6．如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D，过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，EF=$\frac{3}{2}$，则线段CD的长为$\frac{4}{3}$．
分析 由相交弦定理求出FC，由相似比求出BD，设DC=x，则AD=4x，再由切割线定理，BD2=CD•AD求解．
解答 解：由相交弦定理得到AF•FB=EF•FC，即3×1=$\frac{3}{2}$×FC，∴FC=2，
在△ABD中，AF：AB=FC：BD，即3：4=2：BD，BD=$\frac{8}{3}$，
设DC=x，则AD=4x，再由切割线定理，BD2=CD•AD，即x•4x=（$\frac{8}{3}$）2，∴x=$\frac{4}{3}$
故答案为：$\frac{4}{3}$．
点评 本题主要考查了平面几何中直线与圆的位置关系，相交弦定理，切割线定理，相似三角形的概念、判定与性质．
练习册系列答案
相关题目
16．已知$|{\overrightarrow a}|=3$，$|{\overrightarrow b}|=4$，且$\overrightarrow a$与$\overrightarrow b$不共线，若$\overrightarrow a+k\overrightarrow b$与$\overrightarrow a-k\overrightarrow b$垂直时，k的值为（ ）
| A． | -$\frac{3}{4}$ | B． | $\frac{3}{4}$ | C． | ±$\frac{3}{4}$ | D． | ±1 |
已知椭圆C1：$\frac{x^2}{4}+{y^2}$=1的左、右焦点分别是F1、F2，Q是椭圆外的动点，满足|$\overrightarrow{{F_1}Q}$|=4．点P是线段F1Q与该椭圆C1的交点，点T在线段F2Q上，并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0，|$\overrightarrow{T{F}_{2}}$|≠0．
18．如图所示的是一串黑白相间排列的珠子，若按这种规律排列下去，那么第34颗珠子的颜色是（ ）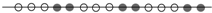
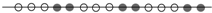
| A． | 白色 | B． | 白色的可能性大 | C． | 黑色 | D． | 黑色的可能性大 |
