题目内容
2.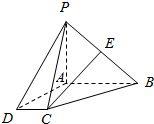 如图,四棱锥P-ABCD中,AB∥CD,AB=2CD,E为PB的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB=2CD,E为PB的中点.(1)求证:CE∥平面PAD.
(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,证明你的结论,若不存在请说明理由.
分析 (1)取PA的中点H,连接EH,DH,证明四边形DCEH是平行四边形,即可证明CE∥平面PAD.
(2)取AB的中点F,连接CF,EF,证明四边形AFCD为平行四边形,可得CF∥AD.又CF?平面PAD,所以CF∥平面PAD,结合(1),即可证明平面PAD∥平面CEF.
解答 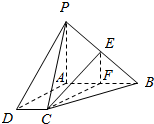 (1)证明:如图所示,取PA的中点H,连接EH,DH.
(1)证明:如图所示,取PA的中点H,连接EH,DH.
因为E为PB的中点,
所以EH∥AB,EH=$\frac{1}{2}$AB.
又AB∥CD,CD=$\frac{1}{2}$AB,
所以EH∥CD,EH=CD.
因此四边形DCEH是平行四边形,
所以CE∥DH.
又DH?平面PAD,CE?平面PAD,
因此CE∥平面PAD.
(2)解:如图所示,取AB的中点F,连接CF,EF,
所以AF=$\frac{1}{2}$AB.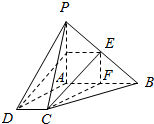
又CD=$\frac{1}{2}$AB,所以AF=CD.
又AF∥CD,所以四边形AFCD为平行四边形,
因此CF∥AD.
又CF?平面PAD,所以CF∥平面PAD.
由(1)可知CE∥平面PAD.
因为CE∩EF=E,故平面CEF∥平面PAD.
点评 此题考查直线与平面平行的判断及平面与平面平行的判断,考查学生分析解决问题的能力,正确证明直线与平面平行是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.为了解某校学生喜爱打篮球是否与性别有关,采用随机抽样方法抽取了50名学生进行问卷调查,得到如下的列联表:
已知在这50名学生中随机抽取1人,抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(Ⅲ)记不喜爱打篮球的5名男生分别为A、B、C、D、E,这5名男生喜爱打乒乓球,
如果从他们当中任选2人作为一对组合参加乒乓球男子双打比赛,求A、B中恰好有1人被选中的概率.
下面的临界值表供参考:
(参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(Ⅲ)记不喜爱打篮球的5名男生分别为A、B、C、D、E,这5名男生喜爱打乒乓球,
如果从他们当中任选2人作为一对组合参加乒乓球男子双打比赛,求A、B中恰好有1人被选中的概率.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17.一个四棱柱的底面是正方形,侧棱与底面垂直,其长度为4,棱柱的体积为16,棱柱的各顶点在一个球面上,则这个球的表面积是( )
| A. | 16π | B. | 20π | C. | 24π | D. | 32π |
12.复数z=$\frac{1}{2+i}$-i2015(i为虚数单位),则$\overline{z}$的虚部为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{4}{5}$i | D. | -$\frac{4}{5}$i |