题目内容

13．设a，b∈R，且$\left\{\begin{array}{l}{（a-1）^3}+2015（a-1）=-2016\\{（b-2）^3}+2015（b-2）=2016\end{array}\right.$，则a+b的值为（　　）
A．0B．1C．2D．3

分析 两式相加，利用立方和公式，即可得出结论．

解答 解：两式相加，得 （a-1）3+（b-2）3+2015（a-1+b-2）=0，
（a+b-3）[（a-1）2+（b-2）2-（a-1）（b-2）+2015]=0
∵（a-1）2+（b-2）2-（a-1）（b-2）+2015=[a-1-$\frac{1}{2}$（b-2）]2+$\frac{3}{4}$（b-2）2+2015＞0
∴a+b-3=0，
∴a+b=3，
故选：D．

点评 本题考查函数的性质，考查立方和公式，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
3．已知D、E分别为△ABC边AB、AC的中点，F是线段DE上一点，BF交AC于点C，CF交AB于点H，求$\frac{AG}{GC}+\frac{AH}{HB}$的值．
4．（1）已知Sn是等差数列{an}的前n项和，且a4=15，S5=55，求过点P（3，a3）、Q（4，a4）的直线的斜率；
（2）设等比数列{bn}的公比q=3，前n项和为Tn，求$\frac{T_4}{b_2}$的值．
1．已知a＞0，若不等式|x-4|+|x-3|＜a在实数集R上的解集不是空集，则a的取值范围是（1，+∞）．
8．函数y=f（x）的图象与直线x=2的交点有几个（　　）
A．1B．0C．0或1D．1或2
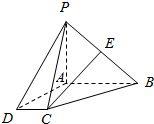18．已知各项不为零的等差数列{an}的公差d≠0，若删去a2，a3，a4，a5的某一项，剩余3项得到的数列（按原来的顺序）是等比数列，则$\frac{{a}_{1}}{d}$的值为-5．
5．对不同的实数值m，讨论直线y=x+m与椭圆$\frac{{x}^{2}}{4}$+y2=1的位置关系．
2．如图，四棱锥P-ABCD中，AB∥CD，AB=2CD，E为PB的中点．
（1）求证：CE∥平面PAD．
（2）在线段AB上是否存在一点F，使得平面PAD∥平面CEF？若存在，证明你的结论，若不存在请说明理由．
3．已知α=-800°．
（1）把α改写成β+2kπ（k∈Z，0≤β＜2π）的形式，并指出α是第几象限角；
（2）求角γ，使γ与角α的终边相同，且γ∈（-$\frac{π}{2}$，$\frac{π}{2}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网