题目内容
20.在二项式($\root{3}{{x}^{2}}$-$\frac{1}{2}$)n的展开式中,只有第5项的二项式系数最大,则n=8;展开式中的第4项为-7${x}^{\frac{10}{3}}$.分析 由条件利用二项式系数的性质求得n=8,再利用二项展开式的通项公式求得展开式中的第4项.
解答 解:在二项式($\root{3}{{x}^{2}}$-$\frac{1}{2}$)n的展开式中,只有第5项的二项式系数${C}_{n}^{4}$最大,则n=8.
展开式中的第4项为T4=${C}_{8}^{3}$•${{(x}^{\frac{2}{3}})}^{5}$•${(-\frac{1}{2})}^{3}$=-7${x}^{\frac{10}{3}}$,
故答案为:8,-7${x}^{\frac{10}{3}}$.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
10.某几何体的三视图如图,则此几何体的体积为( )


| A. | 6 | B. | 34 | C. | 44 | D. | 54 |
15.已知a+b=2,则4a+4b的最小值为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
9.函数f(x)=x2-x-2,x∈[-5,5],在定义域内任取一点x0,使f(x0)>0的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
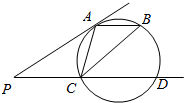 如图,直线PA与圆相切于点A,过P作直线与圆交于C、D两点,点B在圆上,且∠PAC=∠BCD.
如图,直线PA与圆相切于点A,过P作直线与圆交于C、D两点,点B在圆上,且∠PAC=∠BCD.